
第1题:
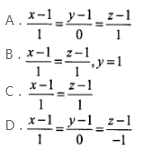
第2题:


第3题:
已知圆22+y2+4x-8y+11=0,经过点P(1,o)作该圆的切线,切点为Q,则线段PQ的长为 ( )
A.10
B.4
C.16
D.8
第4题:

第5题:

第6题:
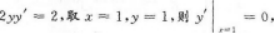
第7题:
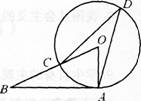
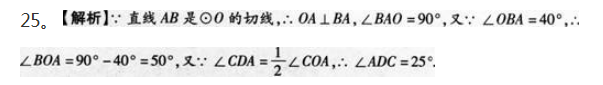
第8题:
已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
y′=3x2-6x,当x=1时,y=1-3-1=-3,即点(1,-3)在曲线上。可知此切线的斜率为k=3×12-6×1=-3,由点斜式可知,此切线的方程为y-(-3)=-3(x-1)即为y=-3x。
第9题:
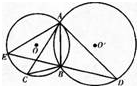
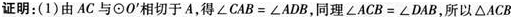

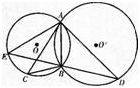
第10题:
