设X在[0,1]上服从均匀分布,Y=2X+1,则下列结论正确的是()
第1题:
A、X+Y服从N(0,1)
B、X+Y不服从正态分布
C、X+Y~X2(2)
D、X+Y也服从正态分布
第2题:
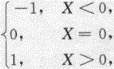 则D(Y)=_______.
则D(Y)=_______.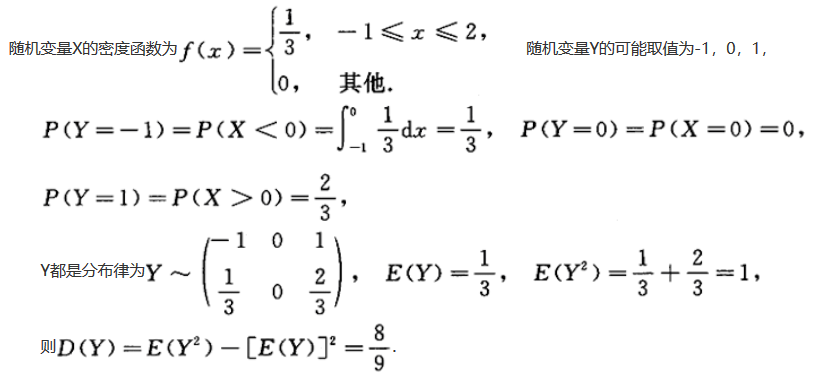
第3题:
设(X,Y)服从在区域D上的均匀分布,其中D为x轴、y轴及x+y=1所围成,求X与Y的协方差Cov(X,Y).

第4题:

第5题:
 在区间(0,1)上服从均匀分布.
在区间(0,1)上服从均匀分布.
第6题:
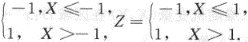 求:
求:

第7题:

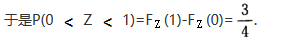
第8题:

第9题:
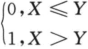 ,V=
,V=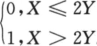 .
.
 .
.
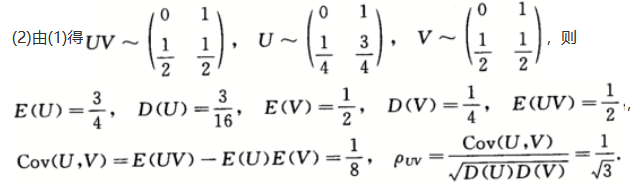
第10题:

