余弦波y=Acosω(1-x/c)在介质中传播,介质密度为ρ0,波的传播过程也是能量传播过程,不同位相的波阵面所携带的能量也不同,若在某一时刻去观察位相为π/2处的波阵面,能量密度为();波阵面位相为π处的能量密度为()。
第1题:
A、波型
B、介质的弹性与密度
C、波的频率
D、以上均不是
第2题:

第3题:
超声波的传播速度取决于
A、波的振动频率
B、介质的弹性
C、介质的密度
D、波的振动周期
E、介质的温度
第4题:
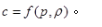
第5题:
第6题:
第7题:
第8题:
此题为判断题(对,错)。
第9题:
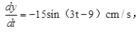
第10题:
传播途径不同,应力波分为两类:在介质内部传播的应力波称为();沿着介质内、外表面传播的应力波称为()。