一自由悬挂的匀质细棒AB,可绕A端在竖直平面内自由转动,现给B端一初速v0,则棒在向上转动过程中仅就大小而言()。
第1题:
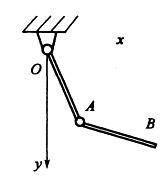
第2题:


第3题:
在沿水平方向的匀强磁场中,有一圆形金属线圈可绕其直径的竖直轴自由转动。开始时线圈静止,线圈平面与磁场方向既不平行也不垂直,所成的锐角为α。在磁场开始增强后
的一个极短时间内,线圈平面( )。
A.维持不动
B.将向使α减小的方向转动
C.将向使α增大的方向转动
D.将转动,因不知磁场方向,不能确定口会增大还是会减小
第4题:

第5题:
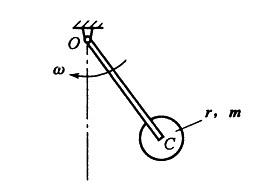

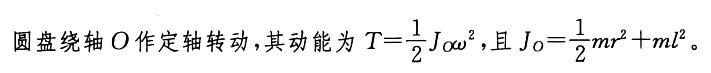
第6题:
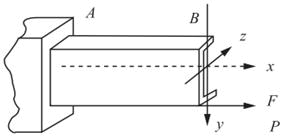
第7题:
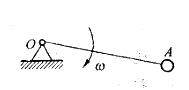

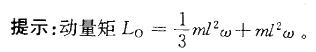
第8题:


第9题:
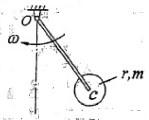
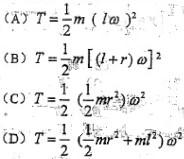
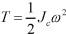 ,其中Jc为刚体通过质心且垂直于运动平面
,其中Jc为刚体通过质心且垂直于运动平面
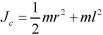 ,带入动能表达式,选(D)。
,带入动能表达式,选(D)。第10题: