发现二项式定理的人是()
第1题:
广义二项式定理在几时发现()
A.1662年
B.1663年
C.1664年
D.1665年
第2题:





第3题:
二项式定理是谁发明的()
A.牛顿
B.莱布尼茨
C.巴罗
D.阿基米德
第4题:
下列科技成就哪些是牛顿取得的()①二项式定理②《关于光和色的新理论》③波动说④《自然哲学中的数学原理》
第5题:
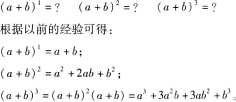

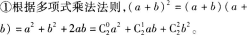




第6题:
发现二项式定理的人是()
A.牛顿
B.哥白尼
C.伽利略
D.开普勒
第7题:


第8题:
二项式定理对发现微积分方法起到了最直接的作用,著名的二项式定理是谁发明的()
A.莱布尼茨
B.牛顿
C.卡迪尔
D.爱因斯坦
第9题:
勤奋和善于钻研是牛顿的性格,有人评价他在大学时代取得的某项成就时说:“即使牛顿没有别的成就,仅这个也足以使他在科学史上留下不朽之名。”该人所评价的牛顿的成就是()
第10题:
()是第一个发现勾股定理的人。