袋中共有5个球,其中3个新球,2个旧球,每次取1个,无放回地取2次,则第二次取到新球的概率是().
第1题:
一个袋内装有10个球,其中有3个白球,5个红球,2个黑球采取不放回抽样,每次取1件,则第二次取到的是白球的概率是()
A、0.6
B、0.5
C、0.4
D、0.3
第2题:
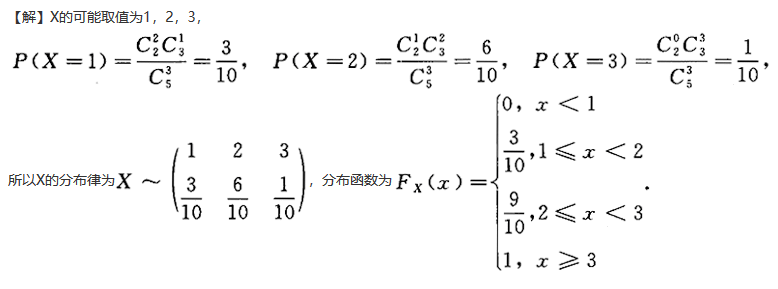
第3题:
A、3/5
B、3/4
C、1/2
D、3/10
第4题:
第5题:

第6题:
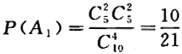
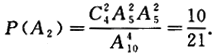
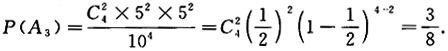
第7题:
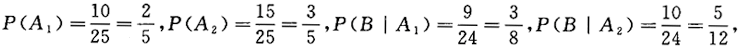
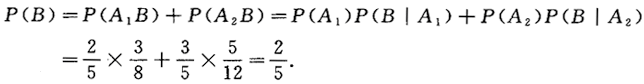
第8题:
一口袋装有6只球,其中4只白球、2只红球。从袋中取球两次,每次随机地取一只。采用不放回抽样的方式,取到的两只球中至少有一只是白球的概率()
A、4/9
B、1/15
C、14/15
D、5/9
第9题:


第10题: