创建一个4阶魔术矩阵A与单位矩阵B,并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。
第1题:
A.二次型xTAx的负惯性指数零
B.存在n阶矩阵C,使得A=CTC
C.A没有负特征值
D.A与单位矩阵合同

第2题:

第3题:
A、可达矩阵
B、单位矩阵
C、加法矩阵
D、零矩阵
第4题:
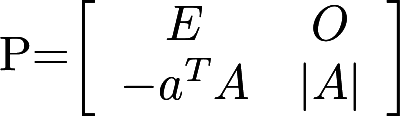 .其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
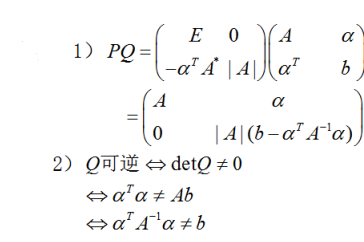
第5题:
 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
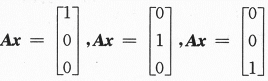 三个方程组的求解问题.
三个方程组的求解问题.


第6题:
A.每块矩阵版提供两个8X4交换矩阵
B.每块矩阵版提供一个8X4交换矩阵
C.每块矩阵版提供两个8X8交换矩阵
D.每块矩阵版提供一个8X8交换矩阵
第7题:
 .
.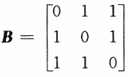 ,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X.
,且矩阵X满足AXA+BXB=AXB+BXA+E,其中E是三阶单位矩阵,求X. ,所以矩阵A-B可逆,且
,所以矩阵A-B可逆,且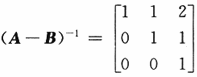 于是.
于是.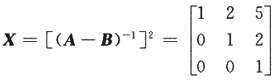
第8题:
A、单位矩阵
B、零矩阵
C、对角矩阵
D、空矩阵
答案:ABCD
解析:特殊矩阵是假若值相同的元素或者零元素在矩阵中的分布有一定规律,则我们称此类矩阵为特殊矩阵。A选项单位矩阵:它的主对角线上是元素1,其余都是0元素;B选项零矩阵:所有的元素都是零元素;C选项对角矩阵:是一个主对角线之外的元素皆为0的矩阵;D空矩阵:没有任何元素的矩阵。这些矩阵的元素都具有一定规律,因此都是特殊矩阵。
第9题:

第10题:
