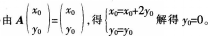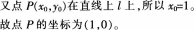(-3,-10)
(3,-10)
(-3,10)
(3,13)
第1题:
此题为判断题(对,错)。
第2题:
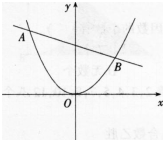


第3题:
对于定义在GF(p)上的椭圆曲线,取素数P=11,椭圆曲线y2=x3+x+6mod11,则以下是椭圆曲线11平方剩余的是()。
A.x=1
B.x=3
C.x=6
D.x=9
第4题:
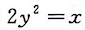 ,求此曲线的方程。
,求此曲线的方程。
第5题:
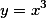 上运动,记坐标原点与点P间的距离为l.若点P的横坐标对时间的变化率为常数
上运动,记坐标原点与点P间的距离为l.若点P的横坐标对时间的变化率为常数 ,则当点P运动到点(1,1)时,l对时间的变化率是
,则当点P运动到点(1,1)时,l对时间的变化率是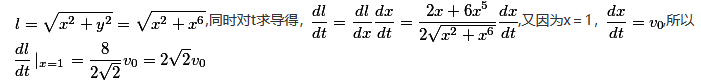
第6题:

第7题:
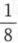 ,P(X=1)=
,P(X=1)=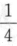 ,在{-1
,在{-1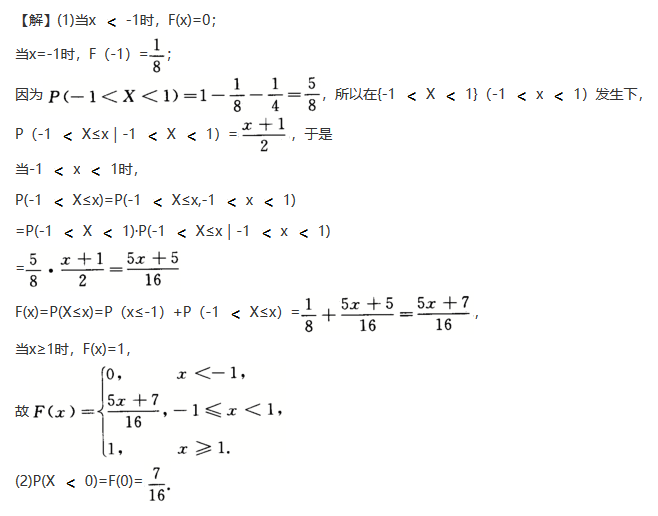
第8题:
已知曲线上的一个点列,求曲线上的其他点的方法称为曲线插值。 ( )
第9题:
 ,其中∑是椭球面S位于曲线C上方的部分.
,其中∑是椭球面S位于曲线C上方的部分.
第10题:
 对应的变换作用下变为直线Z:x+by=l
对应的变换作用下变为直线Z:x+by=l
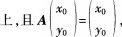 求点P的坐标。
求点P的坐标。