奇函数
偶函数
周期函数
单调函数
第1题:
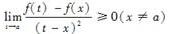


第2题:
第3题:
设R(t)表示可靠度函数,F(t)表示累积故障分布函数,则以下描述正确的是( )。
A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1
B.R(t)是[0,∞]区间内的非增函数,且0≤R(t)≤l
C.在(0,∞)区间内,R(t)+F(t)=l
D.F(t)在[0,∞]区间内的非减函数,且0≤F(t)≤1
E.F(t)在[0,∞]区间内的非增函数
第4题:
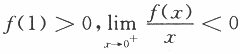 ,证明:
,证明:
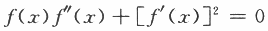 在区间(0,1)内至少存在两个不同实根.
在区间(0,1)内至少存在两个不同实根.
第5题:

第6题:
第7题:
第8题:
设R(t)表示可靠度函数,F(t)表示累积故障分布函数,则下列表述正确的有( )。
A.R(t)是[0,∞)区间内的非减函数,且0≤R(t)≤1
B.R(t)是[0,∞)区间内的非增函数,且0≤R(t)≤1
C.在[0,∞)区间内,R(t)+F(t)=1
D.F(t)在[0,∞)区间内的非减函数,且0≤F(t)≤1
E.F(t)在[0,∞)区间内是非增函数
第9题:
第10题: