违法和不良信息举报 联系客服
免费注册 登录

过点A（1，1，-1），B（-2，-2，2）和C（1，-1，2）三点的平面方程为（）。

题目
单选题
过点A（1，1，-1），B（-2，-2，2）和C（1，-1，2）三点的平面方程为（）。
A

x-3y-2z＝0

B

x+3y-2z-6＝0

C

x-3y+2z+4＝0

D

x+3y+2z-2＝0

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

1×3,2×2,1×1,2×3,1×2,2×1,1×3，…第40项为( )

A.1×3 B.2×3 C.3×1 D.2×1


正确答案：B

第2题：

下面程序的运行结果为( )。def swap(list): temp=list[0] list[0]=list[1] list[1]=templist=[1,2]swap(list)print(list)

A.[1,2]

B.[2,1]

C.[2,2]

D.[1,1]


正确答案：B

第3题：

求椭球面x2+2y2+z2=4在点（1，-1，1）处的切平面方程和法线方程.


正确答案：

 

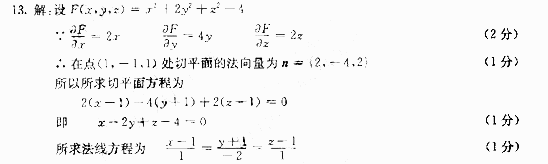
第4题：

过(1，2)点且平行于向量a=(2，2)的直线方程为＿＿＿＿＿．


答案：
解析：
【答案】x-y+1=0 【考情点拨】本题主要考查的知识点为直线的斜截式方式．
【应试指导】设所求直线为L，∵ka=1，L∥a，∴kL=ka=1，又∵L过点(1，2)，∴L的方程为y-2=1×(x-1)，即x-y+1=0．

第5题：

过(1，1，-1)，(-2，-2，2)，(1，-1，2)三点的平面方程是( )。

A.x+3y-2z-6=0
B.x+3y-2z=0
C.x-3y-2z-6=0
D.x-3y-2z=0

答案：D
解析：
设三点依次为A、B、C点，利用三点求两向量，得出所求平面的法向量，再利用平面得点法式方程即可得解

第6题：

下述程序的输出结果是（ ）。

A)2,2

B)1，1

C)3,4

D)1，2


正确答案：D
题干中，*(p)就是数组元素a[O]，输出a[0]，之后指针P的值加1，**q即是数组元素a[l]。

第7题：

过z轴和点M(1，2，-1)的平面方程是：

A. x+2y-z-6=0
B. 2x-y=0
C. y+2z=0
D. x+z=0

答案：B
解析：

第8题：

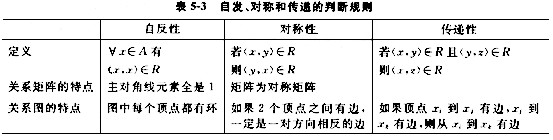
设集合A={1,2,3},下列关系中不是等价关系的为______。A.R1={<1,1>,<2,2>,<3,3>}B.R2={<1,1>,<2,2>

设集合A={1，2，3}，下列关系中不是等价关系的为______。

A．R1={＜1，1＞，＜2，2＞，＜3，3＞}

B．R2={＜1，1＞，＜2，2＞，＜3，3＞，＜2，3＞，＜3，2＞，}

C．R3={＜1，1＞，＜2，2＞，＜3，3＞，＜1，2＞}

D．R4={＜1，1＞，＜2，2＞，＜3，3＞，＜1，2＞，＜1，3＞，＜3，1＞，＜2，3＞，＜3，2＞，}


正确答案：C
解析：设只是非空集合A上的关系，如果R是自反的、对称的和传递的，则称R为A上的等价关系。有关自反、对称和传递的判断规则如表5-3所示。

第9题：

过Z轴和点(1，2，-1)的平面方程是：
(A) χ+ 2y- z- 6 = 0 (B) 2χ-y = 0
(C) y + 2z = 0 (D) χ + z = 0


答案：B
解析：
过Z轴的平面方程可表示为aχ + by = 0，将点(1，2，-1)代入，得a = -2b，即2χ- y = 0。

第10题：

双代号网络图中有（ ）个起点，（ ）个终点。
A、1,1
B、1,2
C、2,1
D、2,2


答案：A
解析：
双代号网络图中有唯一起点，唯一终点。

更多相关问题
相关内容