违法和不良信息举报 联系客服
免费注册 登录

单选题足球比赛中，每一足球队都与其他球队恰好比赛一场，每场比赛胜利的队伍获得2分，输的队伍获得0分，平局双方各得1分。有四位观众统计了所有球队的得分总数分别为2656、2672、2756、2752，经核实，其中有一位观众的统计正确，则参加此次比赛的球队共( )支。A 52B 53C 54D 55

题目
单选题
足球比赛中，每一足球队都与其他球队恰好比赛一场，每场比赛胜利的队伍获得2分，输的队伍获得0分，平局双方各得1分。有四位观众统计了所有球队的得分总数分别为2656、2672、2756、2752，经核实，其中有一位观众的统计正确，则参加此次比赛的球队共(  )支。
A

52

B

53

C

54

D

55

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

在一次象棋比赛中；共有n名选手参加，每位选手都与其他选手恰好比赛一局。每局比赛胜者得2分，负者得0分，平局两位选手各得l分。今有四位同学统计了全部选手的得分总和，分别是238，239，240，242，经核实只有一位同学的统计数据是正确的，正确的数据是（ ）。 A．238 B．239 C．240 D．242


正确答案：C



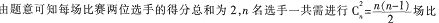
第2题：

140支社区足球队参加全市社区足球淘汰赛，每一轮都要在未失败过的球队中抽签决定比赛对手，如上一轮未失败过的球队是奇数，则有一队不用比赛直接进人下—轮。问夺冠的球队至少要参加几场比赛？

A.3
B.4
C.5
D.6

答案：B
解析：
第一步，本题考查比赛问题。
第二步，根据题意，如果是奇数队的话，有一队轮空，自动进入下一场。题目问冠军至少需要参加几场比赛，为了让冠军参加的场次尽可能的少，每次轮空自动进入下一场的都是冠军。整个比赛过程为：140－70－35－18－9－5－3－2－1，需要进行8轮，有4轮是轮空的。所以冠军至少需要进行4场比赛。

第3题：

4支排球队进行单循环比赛（参加比赛的每两支球队之间都要进行一

场比赛），则总的比赛场数为 _________ 场


正确答案：
6

第4题：

在足球比赛中胜一场得3分，平一场得1分，输一场不得分，如果一个足球队在赛季中得61分，在所有的24场比赛中只输了3场，那么这个球队一共胜了（　　）场。


A. 19
B. 20
C. 21
D. 18

答案：B
解析：
解题指导： 简单计算，输了3场，剩下21场如果全赢为63分，平一场少两分。最后得分为61分，则刚好平一场，胜20场。故答案为B。

第5题：

A、B、C、D、E、F六个球队进行比赛，每两个球队间都要比赛一场。已知A球队已经比赛了5场，B球队已经比赛了4场，C球队已经比赛了3场，D球队已经比赛了2场，E球队已经比赛了1场，则F球队已经比赛了（ ）场。

A.2
B.5
C.3
D.4

答案：B
解析：
根据题干分析，A球队比赛了5场，分别和BCDEF进行比赛，B球队比赛了4场，分别和CDEF进行比赛，同理C队和DEF比赛，D队和EF比赛，E队和F队比赛，那么F球队已经比赛了5场，B项正确，A、C、D选项不符合题意，故本题正确答案选择B项。

第6题：

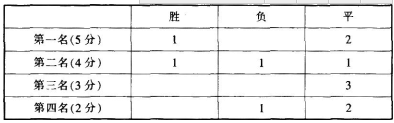
五支曲棍球队进行循环赛，即每两个队之间都要赛一场。每场比赛胜者得2分，输者得o

分，平局两队各得1分。比赛结果各队得分互不相同，并且

(1)第一名的队没有平过；

(2)第二名的队没有输过；

(3)第四名的队没有胜过。

问：全部比赛共平过几场？( )

A．2

B．3

C．4

D．5


正确答案：D
共赛10场，总分为20分。由(1)(2)知，第一名负于第2名，所以第一名至多得6分。又由6+5+4+3+2=20推知，第一名至第五名的得分依次为6、5、4、3、2分。第一名得6分，负于第二名，胜第三、四、五名；
第二名得5分，胜第一名，平三、四、五名；
第三名得4分，已推知负于第一名，平第二、四名，胜第五名；
第四名得3分，由(3)知都是平局得的分，所以负于第一名，平第二、三、五名；
第五名得2分，负于第一、三名，平第二、四名。
所以共有5场平局，分别是第二名与第三名，第二名与第四名，第二名与第五名，第三名与
第四名、第四名与第五名。

第7题：

四支足球队进行单循环比赛，即每两队之间都比赛一场。每场比赛胜者得3分，负者得0分，平局各得l分。比赛结果，各队的总得分恰好是4个连续的自然数。输给第一名的队的总分是多少?

A.2分
B.3分
C.4分
D.5分

答案：C
解析：


场总分在(1+1)×6=12与(3+0)x6=18之间．由于总分是4个连续自然数的和，所以有2+3+4+5=14或3+4+5+6=18两种情况。两种情况均有1支球队得5分．而如果总分为18．那么每场要么得3分要么得0分，单支球趴的积分不可能为5分，所以产生总积分为l4，因此得到各队胜负场次情况见下表：



第三名与所有对手打平，那么第二名输掉的那场对阵第一名．即输给第一名的队总分为4分．选C。

第8题：

在一次围棋比赛中，实行单循环制(即每个选手都与其他选手比赛一局)，每局胜者记2分，输者记0分，如果平局则双方各得1分。今有四位记分员统计了比赛中全部选手的得分总和，结果分别为2005、2004、2070、2008，经核实只有一位记分员统计无误。问这次比赛共有多少名选手参加?（ ） A．44 B．45 C．46 D．47


正确答案：C
假设共有n名选手参加比赛，每位选手恰好与其他选手各比赛一局，即每位选手都要与(n一1)位选手比赛一局，共比赛n(n一1)局。这是从每位选手的角度各自统计

第9题：

世界杯有32支足球队参加比赛。32支球队被分成8个小组，每个小组4支球队。先进行小组赛。在小组赛阶段，各个小组的4支球队进行单循环比赛。小组赛阶段比赛的场次是（ ）场。

A.24
B.36
C.48
D.31

答案：C
解析：
第一步，本题考查比赛问题，用单循环赛公式解题。
第二步，由每个小组4支球队进行单循环比赛，可得每个小组内部的比赛场次数为

第三步，32支球队分成8个小组，每个小组需要进行6场比赛，那么整个小组赛阶段比赛场次数共有8×6＝48（场）。

第10题：

象棋比赛中，每个选手都与其他选手恰好比赛一局，每局胜者记2分，负者记0分，和棋各记1分，四位观众统计了比赛中全部选手得分总数分别是:1979，1980，1983，1985，经核实只有一位观众统计正确，则这次比赛的选手共有多少名?

A. 44
B. 45
C. 46
D. 47

答案：B
解析：
很容易判断比赛总分不可能为奇数，则总分只可能是1980，那么由1980/2=990，所以共进行了990场比赛，设参赛选手为X，(x-1)+(x-2)+...+2+1=990，解得X=45，故答案为B。

更多相关问题
相关内容