1/3
2/9
2/3
1/6
第1题:
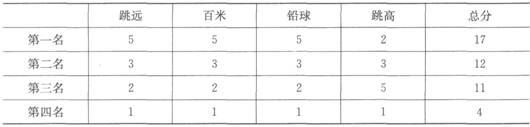
共有4人进行跳远、百米、铅球、跳高4项比赛,规定每个单项中,第一名记5分,第二名记3分,第三名记2分,第四名记1分。已知在每一单项比赛中都没有并列名次,并且总分第一名共获17分,其中跳高得分低于其他项得分;总分第三名共获11分,其中跳高得分高于其他项得分。问总分第二名哪个项目得了第一名?( ) A.跳高 B.百米 C.铅球 D.没有哪个项目得第一名
第2题:
第3题:
第4题:
第5题:
第6题:
第7题:
第8题:
A.跳远
B.接力赛
C.跳高
D.铅球
第9题:
第10题: