ψ=arctan[y/(x-a)]Q/(2π)+arctan[y/(x+a)]Q/(2π)
ψ=arctan[y/(x+a)]Q/(2π)+arctan[y/(x-a)]Q/(2π)
ψ=arctan[(y-a)/x]Q/(2π)+arctan[(y+a)/x]Q/(2π)
ψ=arctan[(y+a)/x]Q/(2π)+arctan[(y-a)/x]Q/(2π)
第1题:
在平面直角坐标系中,标出下列各点:
点A在y轴上,位于原点上方,距离原点2个单位长度;
点B在x轴山,位于原点右侧,距离原点1个单位长度;
点C在x轴上方,y轴右侧,距离每条坐标轴都是2个单位长度;
点D在x轴上,位于原点右侧,距离原点3个单位长度;
点E在x轴上方,y轴右侧,距离x轴2个单位长度,距离y轴4个单位长度。依次连接这些点,你能得到什么图形?
第2题:

第3题:
A、x/y
B、y/x
C、x/(x+y)
D、y/(x+y)
第4题:


第5题:
第6题:
A.该点与原点的连线与X轴夹角为30°
B.该点到原点的距离为30°
C.该点与前一点的连线与X轴夹角为30°
D.该点相对于前一点的距离为30°
第7题:
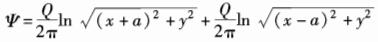
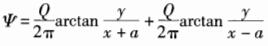
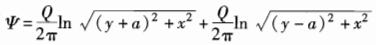
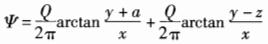
第8题:
坐标“@30<15”中的“30”表示什么()
A.该点与原点的连线与X轴夹角为30°
B.该点到原点的距离为30
C.该点与前一点的连线与X轴夹角为30°
D.该点相对于前一点的距离为30
第9题:
第10题: