第1题:
A 单侧置信下限估计
B 单侧置信上限估计
C 指数估计
D 双侧置信区间估计
第2题:
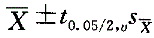
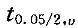 可近似用1.96代替
可近似用1.96代替
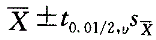
第3题:
在估计某一总体均值时,随机抽取n个单元作样本,用样本均值作估计量,在构造置信区间时,发现置信区间太宽,其主要原因是( )。
A.样本容量太小
B.估计量缺乏有效性
C.选择的估计量有偏
D.抽取样本时破坏了随机性
第4题:
下面有关置信区间和置信水平的说法正确的有()。
第5题:
第6题:
第7题:
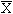 ±t
±t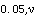 S
S
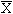 ±t
±t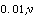 S
S第8题:
以下关于置信区间与精度的关系说法不正确的是
A、当置信度1-α增大,又样本容量n固定时,置信区间长度增加,区间估计精度减低
B、置信区间的长度可视为区间估计的精度
C、当置信度1-α减小,又样本容量n固定,置信区间长度减小,区间估计精度提高
D、置信度1-α固定,当样本容量n增大时,置信区间长度增加,区间估计精度减低
第9题:
第10题:
置信区间和医学参考值范围相比()