违法和不良信息举报 联系客服
免费注册 登录

以下6个图形分别为正方形纸盒的外表面，将其折叠成纸盒后，完全相同的分为一组，分组正确的是：

题目
以下6个图形分别为正方形纸盒的外表面，将其折叠成纸盒后，完全相同的分为一组，分组正确的是：


A.A
B.B
C.C
D.D
参考答案和解析
答案：C
解析：
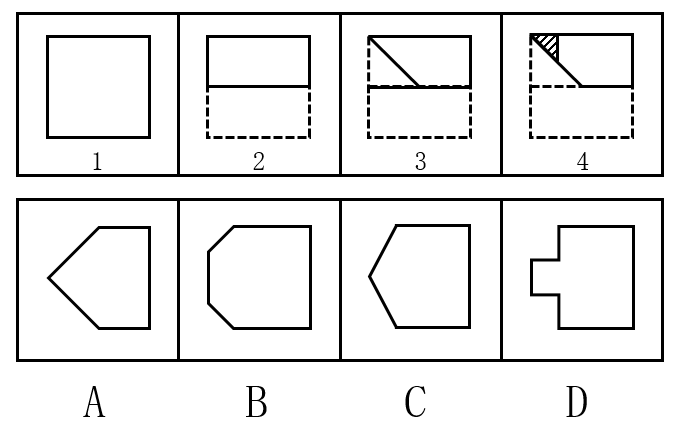
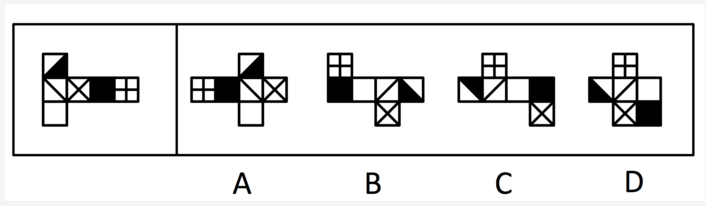
本题考查空间重构。将题干6个图形折叠成纸盒后，完全相同的分为一组，一共分为两组。我们可以通过观察特殊的两个面之间的相邻关系，这两个面之间的相邻关系相同或不同，由此判断出是不是同一个立体图形。我们以①图形为例进行说明。



我们以便于观察的存在一个直角的面，即A面作为基准面进行分析。在折叠过程中，c点与b点会重合，而b点所在的面中，没有从b点引出线。找到其他图形中的A面，再分析c点，通过观察发现，①③④图形中与c点重合的b点没有引出线，而②⑤⑥三个图形中与c点重合的b点引出来一条直线。因此，①③④图形是一组，②⑤⑥三个图形是另外一组。
故正确答案为C。
如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

如下图所示，由图1折叠成图2，再折叠成图3，然后剪去图4的阴影三角部分，现将其完全展开后得到的图形是________。


答案：D
解析：
观察发现，图1至图2为从下往上折，图3将图2折叠产生的矩形的其中一个小正方形沿对角线折叠，图4切掉折叠后图形的一角，实际上切掉的是两个小正方形（如下图所示），因此只有D项符合。
故正确答案为D。

第2题：

以下给定的图形为纸盒的外表面，折叠起来后，应是四个选项中的（ ）。



答案：C
解析：
A 项，正面和右侧面是相对面，不可能相邻，错误；B 项，侧面中的对角线与顶面中对角线应相接，错误；C 项可由左侧图形折成；D 项正面与右侧面应互换。

第3题：

给定纸盒的外表面，下面选项中能由其折叠成的是（ ）


答案：B
解析：
A 选项中两条斜线在右下角不会形成交点，排除；C 选项中心形左侧的斜线方向错误；D 选项斜线位置错误。

第4题：

给定纸盒外表面，下面哪一个图形是由他折成的：



AA
BB
CC
DD


答案：A
解析：
本题考查折纸盒，应从元素的位置特征出发来解题。

B、C中三角阴影的位置错误，D项中直线和叉面的相对位置错误，只有A项各面的位置关系与平面图相符。

故正确答案为A。

第5题：

给定纸盒外表面，下面哪个图形可以和题中图形折成同样的盒子。



AA
BB
CC
DD


答案：B
解析：
本题考查折纸盒，应从元素的位置特征出发来解题。

根据题干给出的平面图展开图，可知黑色一面与叉形一面相邻，A项中这两面是相对的，排除；

C项折叠之后，若以含半个阴影的面为顶面，则折叠之后其他各面与题干给出的平面展开图其他各面的关系相反，排除；

D项折叠后无法形成一个正六面体，排除。

故正确答案为B。

第6题：

以下给定的图形为纸盒的外表面，折叠起来后，应是这四个选项中的（ ）



答案：A
解析：
A 项可由左侧图形折成；B 项，三个面的相对位置错误；C 项，左侧面中的圆的位置错误；D 项，顶面阴影不与右侧面相接，错误。

第7题：

左边给定的纸盒外表面，选项中哪个图形不是由它折叠而成（ ）。



答案：C
解析：
第（1）组，观察给出图形的相对面和相邻面关系，三个三角形构成的两个面分别位于由三个矩形构成的面两边，属于相对面。根据两个相对面中有且只有一个面能够被看到这一特点，可知选C。

第8题：

以下是给定纸盒的外表面，下列哪一个纸盒能由此外表面折叠而成？（ ）



答案：A
解析：
B项的正面和侧面为相对面，不可能相邻，排除;C项正面的斜线应与侧面有公共点，排除;D项正面与侧面的位置反了，排除。只有A项能折成。

第9题：

如图。将其折叠后是一个正方体的纸盒，这个纸盒的底面是______。



A. 1号正方形
B. 2号正方形
C. 3号正方形
D. 4号正方形

答案：B
解析：
解题指导： 可用代入法。当2号正方形为底时，正好围成一个正方体的空盒。故答案为B。

第10题：

左边给定的是纸盒的外表面，以下哪一项能由它折叠而成？


A.A
B.B
C.C
D.D

答案：C
解析：
本题考查空间重构。利用点定位，题干中实线对角线与小黑四边形具有共同的顶点，据此可以排除A、B、D，因此，选择C。

更多相关问题
相关内容