第1题：
第2题：
假设X～N(-1,2),Y～N(1,3)，且X与Y相互独立，则X+2Y～
A、N(1,8)
B、N(1,14)
C、N(1,40)
D、N(1,22)
第3题：
第4题：
第5题：
，反之，如果
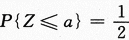，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.
第6题：
A、N(1,2);
B、N(1,4)
C、N(2,4);
D、N(2,5)。
第7题：
设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。
A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则
服从正态分布
B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布
C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布
D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布
第8题：
A、X+Y服从N(0，1)
B、X+Y不服从正态分布
C、X+Y~X2(2)
D、X+Y也服从正态分布
第9题：
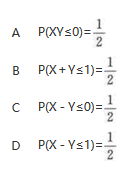
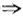P(X+Y≤1)=
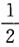，所以选(B).第10题：
。