 的基础解系
的基础解系第1题:
此题为判断题(对,错)。
第2题:
设α1,α2是非齐次线性方程组Ax=b的解.则A(5α2-4α1)=_________.
第3题:
第4题:

第5题:
第6题:
设A是4×6矩阵,r(A)=2,则齐次线性方程组Ax=0的基础解系中所含向量的个数是( )
A.1 B.2
C.3 D.4
第7题:
非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()
第8题:
A、Ax=0只有零解
B、Ax=0的基础解系含r(A)个解向量
C、Ax=0的基础解系含n-r(A)个解向量
D、Ax=0没有解
第9题:
第10题:
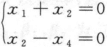 ,(Ⅱ)
,(Ⅱ)
