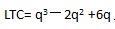第1题:
完全竞争企业的长期成本函数LTC = Q3-6Q2 + 30Q + 40,市场需求函数Qd=204-10P,P=66,试求:
(1)长期均衡的市场产量和利润
(2)这个行业长期均衡时的企业数量
第2题:
第3题:
计算题:Q=6750–50P,总成本函数为TC=12000+0.025Q2。
求:(1)利润最大的产量和价格?
(2)最大利润是多少?
(1)因为:TC=12000+0.025Q2,所以MC=0.05Q
又因为:Q=6750–50P,所以TR=P•Q=135Q-(1/50)Q2
MR=135-(1/25)Q
因为利润最大化原则是MR=MC
所以0.05Q=135-(1/25)Q
Q=1500
P=105
(2)最大利润=TR-TC=89250
第4题:

第5题:

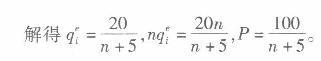
第6题:
已知一垄断企业成本函数为:TC=5Q2 +20Q+1000,产品的需求函数为: Q=140-P,
求:(1)利润最大化时的产量、价格和利润,
(2)厂商是否从事生产?
第7题:
第8题:
假定一个垄断者的产品需求曲线为P=10-3Q,成本函数为TC=Q2+2Q,求垄断企业利润最大时的产量、价格和利润。
TR=P·Q=10Q-3Q2,
则MR=10-6Q,由TC=Q2+2Q,得,MC=2Q+2当MR=MC时,
垄断企业利润最大,即10-6Q=2Q+2,得,Q=1P=10-3×1=7;π=TR-TC=7×1-12-2×1=4
第9题:
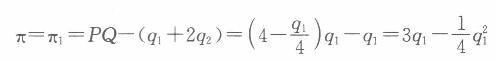
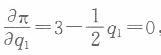
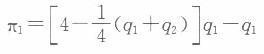
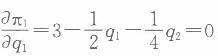
第10题: