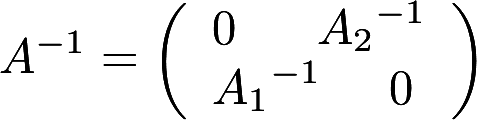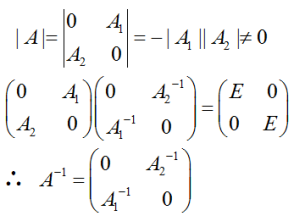第1题:
第2题:
第3题:
某大型整数矩阵用二维整数组 G[1:2M ,l:2N]表示,其中M和N是较大的整数,而且每行从左到右都己是递增排序,每到从上到下也都己是递增排序。元素G[M,N]将该矩阵划分为四个子矩阵A[1:M,1:N],B[1:M,(N+1):2N],C[(M+1):2M,1:N ],D[(M+1):2M,(N+1):2N]。如果某个整数E大于A[M,N],则E( )。
A.只可能在子矩阵A中B.只可能在子矩阵B或C中C.只可能在子矩阵B、C或D中D.只可能在子矩阵D中
第4题:
第5题:
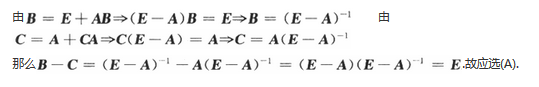
第6题:
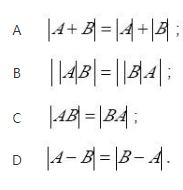
第7题:

第8题:
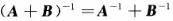

第9题:
第10题:
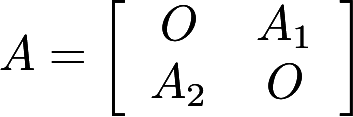 .证明:A可逆,且
.证明:A可逆,且