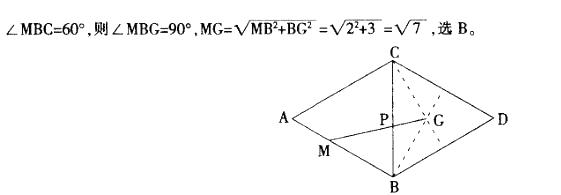
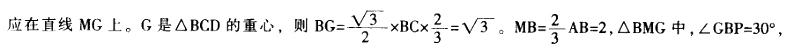第1题:
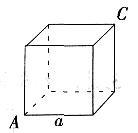
有一只蚂蚁在正方体某条棱的A处,它想尽快地游览完正方体的各个面,然后回到A处,如果正方体的棱长为10cm,则这只蚂蚁通过的最短路程为( )。
A. 55cm B. 30 cm C. 120cm D. 42 cm
第2题:


第3题:
当小虫进入婴儿耳内,可让婴儿捂住双耳,憋死小虫。()
第4题:
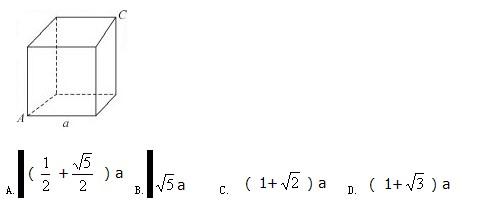
第5题:
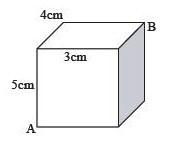

第6题:
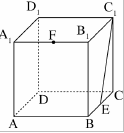
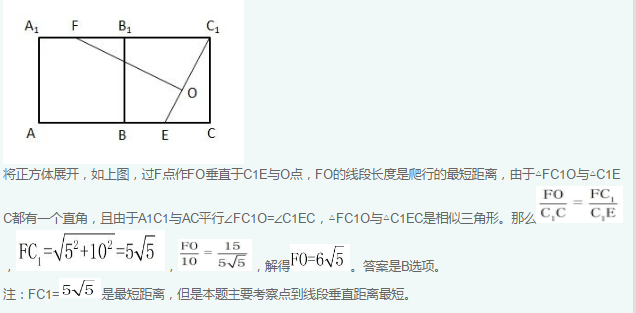
第7题:
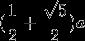
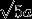

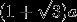
 。
。第8题:
如图所示,有一只蚂蚁在正方体某条棱的A处,它想尽快地游览完正方体的各个面,然后回到A处,如果正方体的棱长为10cm,则这只蚂蚁通过的最短路程为( )。
A. 55cm
B. 30 cm
C. 120cm
D. 42 cm
第9题:
 厘米,底面半径为6厘米,一只蚂蚁从A.点沿圆锥侧面爬行到B.点,则最短的距离为_________厘米。
厘米,底面半径为6厘米,一只蚂蚁从A.点沿圆锥侧面爬行到B.点,则最短的距离为_________厘米。




第10题: