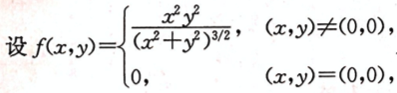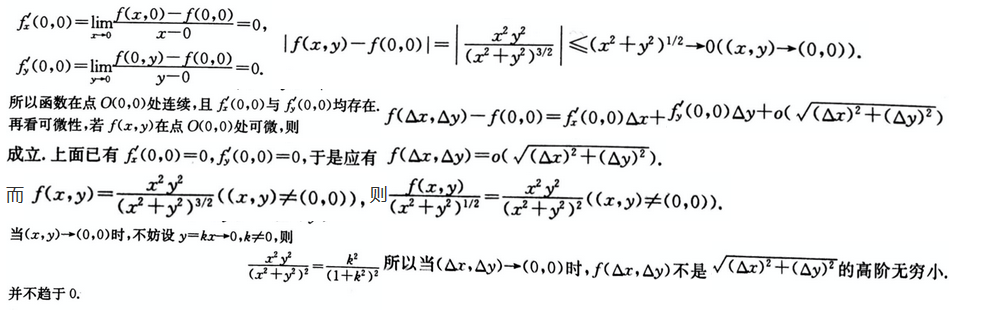1834年有位数学家发现了一个处处连续但处处不可微的函数例子,这位数学家是()。
第1题:
处处与重力方向垂直的连续曲面称为水平面。()
第2题:
A.处处相等
B.只能保证傅氏级数系数有界
C.除f(t)不连续的t值外,处处相等
D.处处不相等,但能量相同
第3题:
请结合例子简要谈谈“生活中处处有数学”。

第4题:
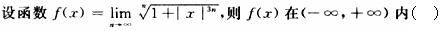

第5题:
A、处处相等
B、只能保证傅氏级数系数有界
C、除f(t)不连续的t值外,处处相等
D、处处不相等,但能量相同
第6题:
A.不可压缩流动
B.处处无旋
C.任意平面
D.平面连续
第7题:
()是一个处处与重力方向垂直的连续曲面。
A.海平面
B.水平面
C.水准面
D.竖直面
第8题:
水准面是处处与铅垂线()的连续封闭曲面。
第9题:
只有每一个射野内诸点的剂量率能够按要求的方式进行调整(调强)才能使:()。
A.靶区内的剂量处处相等
B.靶区表面的剂量处处相等
C.靶区内及表面的剂量处处相等
D.临床靶区内的剂量处处相等
E.计划靶区内的剂量处处相等
第10题: