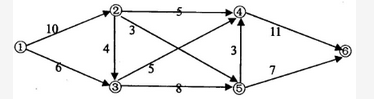
试题解析:本题考查应用数学基础知识。
从站点①到⑥有多条线路。显然,每条线路上的最大流量等于该线路上各段管道最大流量的最小值。站点①到⑥的最大总流量等于所有线路最大流量之和。
我们可以先从流量较大的线路开始计算。例如,线路①②④⑥的最大流量为min(10,5,11)=5。线路①③⑤⑥的最大流量为min(6,8,7)=6。除去这两条线路的流量后,剩余流量的图示如下:
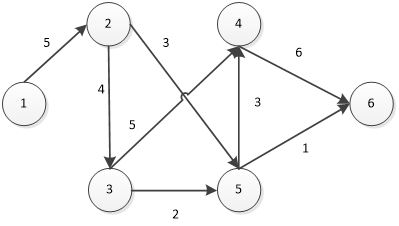
根据此图,线路①②③④⑥的最大流量为mm(5,4,5,6)=4。除去该线路上的流量后得:
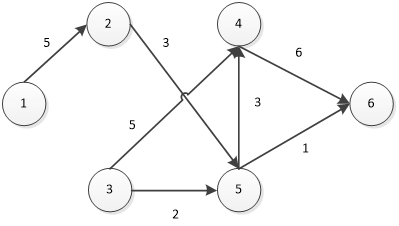
根据此图,线路①②⑤⑥的最大流量为min(1,3,1)=1。除去该线路上的流量后,从①到⑥已不连通,也就不再有剩余流量。
汇总后,最大总流量可以达到5+6+4+1=16(百吨/小时)。上述实现最大流量的方法是:
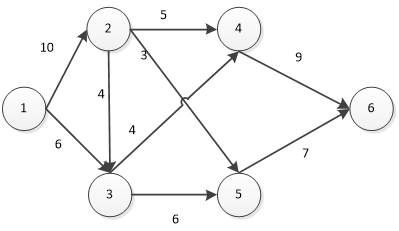
该图中,各管道的实际流量都不超过其最大流量。除起点和终点外,所有站点的进油量等于其出油量。
虽然解答此题可以有多种选择线路的方案,但计算得到的最大总流量值都是-致的。
由于上述解题过程中,管道⑤一④尚未用到,因此,该管道的关闭并不会影响最大总流量值。其他路段管道的关闭是否会影响总流量值呢?
为了保持总流量值为16,从①出发的两段管道必须满负苟运输。管道①一②的流量10被分散到②一③、②一④、②一⑤三条管道,关闭其中任何一条管道都将达不到流量为10。同时,管道②一③的流量至少为2。
同样,为保持最大总流量,管道①一③的流量为6,管道③一⑤显然不能关闭。假设管道③一④关闭,则管道④一⑥的流量至多为8,到达站点⑥的流量至多为15。所以为保持最大总流量,管道③一④不能关闭。
为保持到达站点⑥的总流量为16,显然管道④一⑥和⑤一⑥任何一个都不能关闭。从而,只有管道⑤一④的关闭对最大总流量没有影响。