设λ1,λ2是矩阵A的两个不同的特征值,ξ、η是a的分别属于λ1、λ2的特征向量,则以下选项正确的是()。
第1题:
A.3是A的特征值
B.-3是A的特征值
C.1/3是A的特征值
D.-1/3是A的特征值
答案:D
解析:E+3A不可逆,即∣E+3A∣=0,即-3 * ∣(-1/3)E-A∣=0,所以A的特征值为-1/3。
第2题:
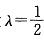 是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
是非奇异矩阵A的特征值,则矩阵(2A3)- 1有一个特征值为:
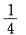
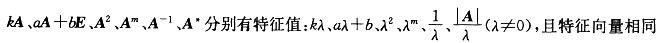

第3题:
A、3,5
B、1,2
C、1,1,2
D、3,3,5
第4题:
第5题:


第6题:
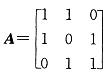 ,则A的特征值是:
,则A的特征值是:


第7题:
第8题:
A、-1
B、-2
C、1
D、2
第9题:

第10题: