N（μ，σ2）为（）A、正态分布B、标准正态分布C、卡方分布D、二项分布E、泊松分布

题目

N（μ，σ2）为（）

A、正态分布
B、标准正态分布
C、卡方分布
D、二项分布
E、泊松分布

如果没有搜索结果或未解决您的问题，请直接联系老师获取答案。

相似问题和答案

第1题：

假设线性表的长度为n，则在最坏情况下，冒泡排序需要的比较次数为（）。A．log2n B．n2 C．n/2 D．n(n-1)/2

正确答案：D
冒泡排序；依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。至此第一趟结束，将最大的数放到了最后。在第二趟：仍从第一对数开始比较（因为可能由于第2个数和第3个数的交换，使得第1个数不再小于第2个数），将小数放前，大数放后，一直比较到倒数第二个数（倒数第一的位置上已经是最大的），第二趟结束，在倒数第二的位置上得到一个新的最大数（其实在整个数列中是第二大的数）。如此下去，重复以上过程，直至最终完成排序。

第2题：

n＋1位有符号数x的补码表示范围为A.－2n

n+1位有符号数x的补码表示范围为

A.－2n

B.－2n≤x≤2n-1

C.－2n-1≤x≤2n-1

D.－2n≤x<2n-1

正确答案：B

第3题：

已知数列{an}满足an=3n+1(n为奇数，n∈N) 2n-2（n为偶数，n∈N）则a2·a3=（）。

A．70

B．28

C．20

D．8

正确答案：C
简单代入解题。a2=2×2-2=2，a3=3×3+1=10，故a2·a3=20。
［名师点评］像这种简单题，最好要做到秒杀。

第4题：

在图示四个轴力N1、N2、N3和N4中，( )。

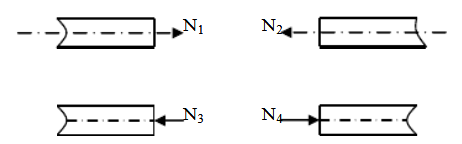
：(A)N1和N2为正，N3和N4为负。

(B)N1和N4为正，N2和N3为负。

(C)N2和N3为正，N1和N4为负。

(D)N3和N4为正，N1和N2为负

正确答案：A

第5题：

一个算法的语句执行次数为(2n2+2nlog2n+4n-7)，则其时间复杂度为()。

A.O(n2)

B.O(nlog2n)

C.O(n)

D.O(2n2)

正确答案：A

第6题：

在一棵二叉树上，度为零的节点的个数为n0，度为2的节点的个数为n2，则n0的值为

A．n2+1

B．n2-1

C．n2

D．n2/2

正确答案：A
解析：度为零的节点即为二叉树的叶子，所以根据二叉树的基本性质3(设二叉树叶子数为 n0，度为2的节点数为n0=n2+1) ，可知n0=n2+1。

第7题：

若在一棵排序二叉树中叶结点的数目为n0，度为2的结点数目为n2，那么n0、n2之间满足（）。A．n0=2n2B．n0= n2-1C．n0= n2+1D．2n0= n2

正确答案：C
依据二叉树的特点，度为0（叶子结点）的个数n0和度为2的结点个数n2的关系为：n0=n2+1。

第8题：

关于主对角线(从左上角到右下角)对称的矩阵为对称矩阵;如果一个矩阵中的各个元素取值为0或1，那么该矩阵为01矩阵，求大小为N*N的01对称矩阵的个数?()

A.power(2,n);

B.power(2,n*n/2);

C.power(2,(n*n+n)/2);

D.power(2,(n*n-n)/2);

正确答案：C

第9题：

在一棵二叉树中,度为零的结点的个数为n0,度为2的结点的个数为n2,则有n0=()

A、n2

B、n2+1

C、n2-1

D、n2+2

参考答案：B

第10题：

在最坏情况下，下列各排序方法的比较次数正确的是

A．冒泡排序为n/2

B．冒泡排序为n(n+1)/2

C．快速排序为n/2

D．快速排序为n(n-1)/2

正确答案：D
解析：在最坏情况下，冒泡排序的比较次数为n(n-1)/2，快速排序的比较次数也为n(n-1)/2。

N（μ，σ2）为（）

题目

相似问题和答案

更多相关问题

相关内容