违法和不良信息举报 联系客服
免费注册 登录

设参考序列为 Y0=（8，8.8，16，18，24，32），被比较序列为 Y1=（10，11.16，18.34，20，23.4，30） Y2=（5，5.625，5.375，6.875，8.125，8.75） 求其关联度。

题目

设参考序列为 Y0=（8，8.8，16，18，24，32），被比较序列为 Y1=（10，11.16，18.34，20，23.4，30） Y2=（5，5.625，5.375，6.875，8.125，8.75） 求其关联度。

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

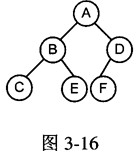
若二叉树的先序遍历序列为ABCEDF，后序遍历序列为CEBFDA，则其中序遍历序列为(65)。

A．CEFBDA

B．CBEAFD

C．CEBAFD

D．CBEDFA


正确答案：B
解析：对于二叉树遍历序列有一个性质，包含有中序遍历序列的任意两个遍历序列可以唯一确定该二叉树。那么由题中的先序遍历序列和后序遍历序列就可以唯一确定此二叉树，如图3-16所示，再对其进行中序遍历，中序遍历序列为CBEAFD。

第2题：

若二叉树的先序遍历序列为ABDECF，中序遍历序列为DBEAFC，则其后序遍历序列为(8)。

A．DEBAFC

B．DEFBCA

C．DEBCFA

D．DEBFCA


正确答案：D
解析：本题要求根据二叉树的先序遍历和中序遍历求后序遍历。我们可以根据这棵二叉树的先序和中序遍历画出这棵二叉树，然后再得出其后序遍历结果。根据先序和中序来构造二叉树的规则是这样的：首先看先序遍历序列ABDECF，先序遍历中第一个访问的结点是A，这说明A是二叉树的根结点(因为先序遍历顺序是：根，左，右)。然后看中序遍历序列DBEAFC，中序中A前面有结点DBE，后面有结点FC。这说明DBE是A的左子树，FC是A的右子树(因为中序遍历顺序是：左，根，右)。再回到先序遍历序列中看DBE的排列顺序(此时可以不看其他的结点)，我们发现在先序遍历序列中B排在最前面，所以B是A的左子树的根结点。接下来又回到了中序遍历序列，中序遍历序列中D在B的前面，E在B的后面，所以D是B的左子树，E是B的右子树。对于A的右子树，可同样依此规则得出。由此，可构造二叉树，如图4-8所示。然后对这棵二叉树进行后序遍历，得到DEBFCA。

第3题：

设某二叉树的前序序列为ABC，中序序列为CBA，则该二叉树的后序序列为()。

A.BCA

B.CBA

C.ABC

D.CAB


正确答案：B

第4题：

若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为______。

A．DEBAFC

B．DEFBCA

C．DEBCFA

D．DEBFCA


正确答案：D

第5题：

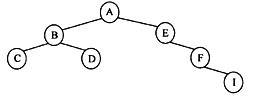
已知某二叉树的中序序列为CBDAEFI、先序序列为ABCDEFI，则该二叉树的高度为(58)。

A．2

B．3

C．4

D．5


正确答案：C
解析：本题考查二叉树的遍历运算。根据二叉树的定义，非空二叉树由根结点、根的左子树和根的右子树三部分组成。二叉树的先序遍历定义为：先访问根结点，然后先序遍历根的左子树，最后先序遍历根的右子树。二叉树的中序遍历定义为：中序遍历根的左子树，访问根结点，最后中序遍历根的右子树。由此，根据二叉树的先序遍历序列和中序遍历序列构造二叉树时，首先根据先序序列找到根结点，然后由中序序列分别得到左、右子树的中序序列和先序序列，如此反复进行分解，即可得到原二叉树。因该二叉树的先序序列中A是第一个结点，因此确定A是整棵二叉树的树根，在中序序列中找到A，并据此划分出根的左子树上的结点中序序列CBD和右子树上的结点中序序列EFI。再根据先序遍历的特点，先序序列指示出B是左子树的根结点，中序序列中C在B的左边、D在B的右边，因此确定C结点在以B为根的左子树上、D结点在以B为根的右子树上。依次类推，根据先序序列确定根，根据中序序列分割子树，最后得到的原二叉树如下图所示。

二叉树的层数为树的高度。

第6题：

若已知一棵二叉树先序序列为ABCDEFG,中序序列为CBDAEGF,则其后序序列为()。

:ACDBGFEA

BCDBFGEA

CCDBAGFE

DBCDAGFE


参考答案：A

第7题：

一棵二叉树的先序遍历序列为ABCDEF,中序遍历序列为CBAEDF,则后序遍历序列为()。

A.CBEFDA

B.FEDCBA

C.CBEDFA

D.不确定


参考答案：A

第8题：

若二叉树的先序遍历序列为ABDECF，中序遍历序列DBEAFC，则其后序遍历序列为(40)。

A．DEBAFC

B．DEFBCA

C．DEBCFA

D．DEBFCA


正确答案：D
解析：对于二叉树遍历序列有一个性质：包含有中序遍历序列的任意两个遍历序列可以唯一确定该二叉树。那么由题中的先序遍历序列和中序遍历序列就可以唯一确定此二叉树如下图所示，再对其进行后序遍历即可。

第9题：

已知二叉树的中序序列为DBEACPC，先序序列为ABDECPC，则后序序列为(17)。

A．DEBACFC

B．DEFCBCA

C．DEBCFCA

D．DEBCFCA


正确答案：D
解析：二叉树的先序序列为ABDECPG，所以根结点为A，于是根据中序序列为DDEAGPC可知，A前面的DBE元素是左于树的，右面的FC是右子树上的，于是可以得到左右子树的中序序列和先序序列。按照此方法进行下去，最终得到树的结构。对树进行后序遍历可得DEBGPCA。

第10题：

已知二叉树的前序序列为ABDCEFG，中序序列为DBCAFEG，则后序序列为______。

A． DCBAFGE

B．DCBFGEA

C．DCBFEGA

D．DCBGFEA


正确答案：B

更多相关问题
相关内容