P（6，4）
P（4，6）
P（5，6）
P（6，5）
第1题：
下述关于Bezier 曲线P l (t) , P 2 (t) , t ∈[ 0 , l ]的论述,哪个是错误的?( )
A. P 1(l) = P 2(0) = P ,在P 处P l (l) 、P 2(0)的切矢量方向相同,大小相等,则P 1(t) 、P 2(t) 在⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111010002TP 处具有G1连续
B. P1(l) = P2(0) = P ,在P 处P l(l)、P2(0)的切矢量方向相同,大小相等,则P1(t) 、P2(t) 在
P 处具有C l连续
C. 若保持原全部顶点的位置不变,只是把次序颠倒过来,则新的Bezier 曲线形状不变,但方向相反
D. 曲线的位置和形状只与特征多边形的顶点的位置有关,它不依赖坐标系的选择
第2题：
A.450.000
B.500.000
C.550.000
D.586.603
第3题：
A.(8，6，2)
B.(8，6)
C.(4，3，1)
D.(4，3)
第4题：
则点P的坐标为( )
第5题：
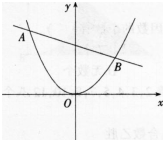
第6题：
下面程序的输出结果是( )。 #include ＜iostream＞ using namespace std; class point { public: point(int px=10,int py=10){ x=px;y=py;} getpx( ) { return x;} getpy( ) { return y;} private: int x,y; }; void main(voiD) { point p,q(15,15); cout＜＜"p点的坐标是:"＜＜p. getpx( )＜＜" ,"; cout＜＜p. getpy( )＜＜endl; cout＜＜"q点的坐标是:"＜＜q. getpx( )＜＜" ,"; cout＜＜q. getpy( ); }
A．p点的坐标是:10,10 q点的坐标是:15,15
B．p点的坐标是:0,0 q点的坐标是:15,15
C．p点的坐标是:0,0 q点的坐标是:0,0
D．p点的坐标是:10,10 q点的坐标是:10,10
第7题：
在平面直角坐标系中选择一些横、纵坐标满足下面条件的点，标出它们的位置，看看它们在第几象限或哪条坐标轴上：
（1）点P（x，y）的坐标满足xy＞0；
（2）点P（x，y）的坐标满足xy＜0；
（3）点P（x，y）的坐标满足xy=0；
（1）在第一、三象限的点P（x，y）的坐标满足xy＞0；
（2）在第二、四象限的点P（x，y）的坐标满足xy0；
（3）在x轴上或者y轴上的点P（x，y）的坐标满足xy=0；
第8题：
矢量数据格式：矢量格式是一种以纪录空间坐标的方法表示地表各种点、线、面实体的空间数据结构。与栅格数据相比，矢量格式能较为精确地表达地理实体(其精度仅受数字化仪的精度及数值纪录字长的限制)。()
第9题：
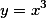上运动，记坐标原点与点P间的距离为l.若点P的横坐标对时间的变化率为常数
,则当点P运动到点(1,1)时，l对时间的变化率是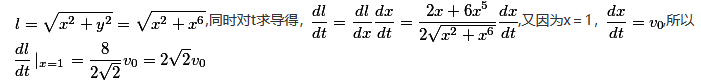
第10题：
