第1题:

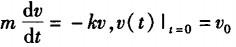


第2题:

第3题:
(6分)物体只在重力作用下由静止开始下落的运动称为自由落体运动”。小明对这种落体运动产生了探究的兴趣,提出如下两个问题。
问题一:物体下落的快慢是否与物体的质量有关?问题二:物体下落的高度与下落的时
间存在着怎样的关系?于是他找来一些器材并在可忽略空气阻力情况下准备进行实验。
(1)请你帮助小明设计探究“问题一”的实验方案。
(2)小明探究“问题二”时,通过实验,测量出同一物体分别从最高点下落的高度为hl、h2、h3,并测量出每次下落的高度所对应的下落时间为fl、f2、f3。分析实验数据发现:“物体下落的高度与下落的时间不满足正比例关系”。他猜想“物体下落的高度与下落的时间平方成正比”,若要验证这一猜想,应如何处理分析实验数据?

第4题:
第5题:
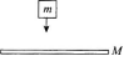
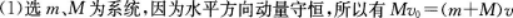

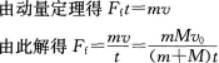
第6题:
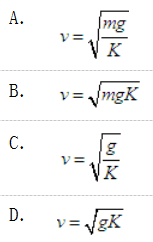

第7题:
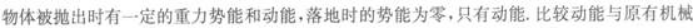

第8题:
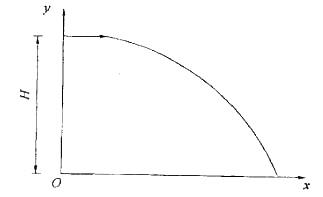
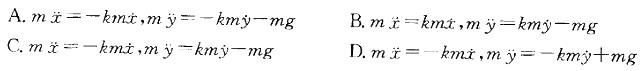
第9题:
第10题:
