违法和不良信息举报 联系客服
免费注册 登录

单选题下列说法不正确的是（　　）。A s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则加入k个n维向量β(→)1，β(→)2，…，β(→)k后的向量组仍然线性无关B s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则每个向量增加k维分量后得到的向量组仍然线性无关C s个n维向量α(→)1，α(→)2，…，α(→)s线性相关，则加入k个n维向量β(→)1，β(→)2，…，β(→)k后得到的向量组仍然线性相关D s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则减少一个向

题目
单选题
下列说法不正确的是（　　）。
A

s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则加入k个n维向量β(→)1，β(→)2，…，β(→)k后的向量组仍然线性无关

B

s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则每个向量增加k维分量后得到的向量组仍然线性无关

C

s个n维向量α(→)1，α(→)2，…，α(→)s线性相关，则加入k个n维向量β(→)1，β(→)2，…，β(→)k后得到的向量组仍然线性相关

D

s个n维向量α(→)1，α(→)2，…，α(→)s线性无关，则减少一个向量后得到的向量组仍然线性无关

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

3维向量组A：a1，a2，…，am线性无关的充分必要条件是( ).

A.对任意一组不全为0的数k1，k2，…，km，都有k1a1+k2a2+…+kmam≠0
B.向量组A中任意两个向量都线性无关
C.向量组A是正交向量组
D.

答案：A
解析：
B与D是向量组线性无关的必要条件，但不是充分条件.C是向量组线性无关的充分条件，但不是必要条件.A是向量组线性无关定义的正确叙述，即不存在一组不全为零的数k1，k2，…，km，使得k1a1+k2a2+…+kmam=0.故选A.

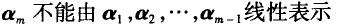
第2题：

3维向量组A：α1，α2，…，αM线性无关的充分必要条件是（）．

  • A、对任意一组不全为0的数k1，k2，…，kM，都有后
  • B、向量组A中任意两个向量都线性无关
  • C、向量组A是正交向量组
  • D、αM不能由线性表示

正确答案:A

第3题：

若a1,a2,……an是一个线性无关的n维向量组,则任何n维向量均可由它们线性表示。()

此题为判断题(对，错)。


参考答案：正确

第4题：

单选题
下列说法不正确的是（　　）.
A

s个n维向量α1，α2，…，αs线性无关，则加入k个n维向量β1，β2，…，βk后的向量组仍然线性无关

B

s个n维向量α1，α2，…，αs线性无关，则每个向量增加k维分量后得到的向量组仍然线性无关

C

s个n维向量α1，α2，…，αs线性相关，则加入k个n维向量β1，β2，…，βk后得到的向量组仍然线性相关.

D

s个n维向量α1，α2，…，αs线性无关，则减少一个向量后得到的向量组仍然线性无关.


正确答案： B
解析：
A项，一个线性无关组加入k个线性相关的向量，新的向量组线性相关；B项，线性无关组的延伸组仍为线性无关组；C项，线性相关组加入k个向量，无论k个向量是否相关，构成的新的向量组必是线性相关的；D项，线性无关组中的任意个组合均是无关的．

第5题：

单选题
n维向量组，α(→)1，α(→)2，…，α(→)s（3≤s≤n）线性无关的充要条件是（　　）。
A

存在一组不全为0的数k1，k2，…，ks，使kα(→)1＋k2α(→)2＋…＋ksα(→)s≠0(→)

B

α(→)1，α(→)2，…，α(→)s中任意两个向量都线性无关

C

α(→)1，α(→)2，…，α(→)s中存在一个向量不能由其余向量线性表示

D

α(→)1，α(→)2，…，α(→)s中任何一个向量都不能由其余向量线性表示


正确答案： C
解析：
向量组线性相关的充要条件是其中至少有一个向量可以由其余向量表示，若向量组中任何一个向量都不能由其余向量线性表示，则它们必线性无关；反之亦然。

第6题：

设向量组I：α1α2αr…，可由向量组Ⅱβ1,β2,…βs：线性表示，下列命题正确的是( )。

A.若向量组I线性无关．则r≤S
B.若向量组I线性相关，则r>s
C.若向量组Ⅱ线性无关，则r≤s
D.若向量组Ⅱ线性相关，则r>s

答案：A
解析：
由于向量组I能由向量组Ⅱ线性表示，所以r(I)≤r(Ⅱ)，即

第7题：

单选题
设n维列向量组α1，α2，…，αm（m＜n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（　　）.
A

向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示

B

向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示

C

向量组α1，…，αm与向量组β1，…，βm等价

D

矩阵A=（α1，…，αm）与矩阵B=（β1，…，βm）β）m


正确答案： C
解析：
例如α1=（1，0，0，0），α2=（0，1，0，0），β1=（0，0，1，0），β2=（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β1，β2，…，βm线性无关．

第8题：

设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明：向量β为零向量.


答案：
解析：

第9题：

单选题
设n阶方阵A＝（α(→)1，α(→)2，…，α(→)n），B＝（β(→)1，β(→)2，…，β(→)n），AB＝（γ(→)1，γ(→)2，…，γ(→)n），记向量组（Ⅰ）：α(→)1，α(→)2，…，α(→)n；（Ⅱ）： β(→)1，β(→)2，…，β(→)n；（Ⅲ）：γ(→)1，γ(→)2，…，γ(→)n。如果向量组（Ⅲ）线性相关，则（　　）。
A

向量组（Ⅰ）与（Ⅱ）都线性相关

B

向量组（Ⅰ）线性相关

C

向量组（Ⅱ）线性相关

D

向量组（Ⅰ）与（Ⅱ）中至少有一个线性相关


正确答案： A
解析：
由向量组（Ⅲ）线性相关，知矩阵AB不可逆，即|AB|＝|A|·|B|＝0，因此|A|、|B|中至少有一个为0，即A与B中至少有一个不可逆，故向量组（Ⅰ）与（Ⅱ）中至少有一个线性相关。

第10题：

单选题
设n维列向量组α(→)1，α(→)2，…，α(→)m（m＜n）线性无关，则n维列向量组β(→)1，β(→)2，…，β(→)m线性无关的充分必要条件是（　　）。
A

向量组α(→)1，α(→)2，…，α(→)m可以由β(→)1，β(→)2，…，β(→)m线性表示

B

向量组β(→)1，β(→)2，…，β(→)m可以由α(→)1，α(→)2，…，α(→)m线性表示

C

向量组α(→)1，α(→)2，…，α(→)m与向量组β(→)1，β(→)2，…，β(→)m等价

D

矩阵A＝（α(→)1，α(→)2，…，α(→)m）与矩阵B＝（β(→)1，β(→)2，…，β(→)m）等价


正确答案： D
解析：
例如α(→)1＝（1，0，0，0），α(→)2＝（0，1，0，0），β(→)1＝（0，0，1，0），β(→)2＝（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；
D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β(→)1，β(→)2，…，β(→)m线性无关。

更多相关问题
相关内容