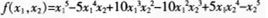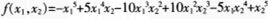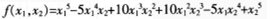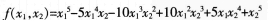第1题：
已知函数f(x)=(a+1)lnx+ax2+1.
(Ⅰ)讨论函数f(x)的单调性；
(Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.
第2题：
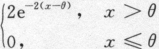,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
第3题：
A、X1(f)X2(f)
B、X1(f)*X2(f)
C、X1(-f)X2(-f)
D、X1(-f)*X2(-f)
第4题：
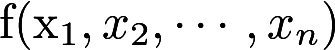都使f＞0，问f是否必然正定?
第5题：
,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ；(2)求D(θ).
第6题：
第7题：
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.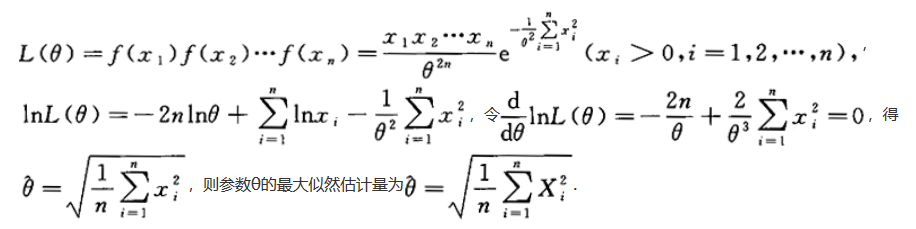
第8题：
请补充main函数，该函数的功能是求方程ax2+bx+c=0的根(方程的系数a,b,c从键盘输入)。
例如， 当a=1，b=2，c=1时， 方程的两个根分别是：
x1=-1.00,x2=-1.00。
注意：部分源程序给出如下。
请勿改动主函数main和其他函数中的任何内容，仅在 main函数的横线上填入所编写的若干表达式或语句。
试题程序：
include ＜stdio.h＞
include ＜conio.h＞
include ＜math.h＞
main()
{
float a，b，c，disc，x1，x2，p，q；
scanf("%f，%f，%f"，&a，&b，&c)；
disc=b*b-4*a*c；
clrscr()；
printf("****** the result ****+*+\n")；
if(disc＞=0)
{
x1=【 】；
x2=(-b-sqrt(disc))/(2*a)；
printf("x1=%6．2f，x2=%6.2f\n"，x1，x2)；
}
else
{
p=【 】；
q=【 】；
printf("x1=%6.2f+%6.2f i\n"，p，q)；
printf("x2=%6.2f-%6.2f i\n"，p，q)；
}
}
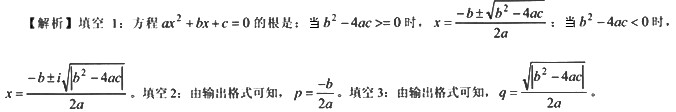
第9题：
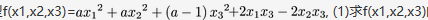, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为
. 求a
第10题：
