给定两个正整数m=630和n=675．利用辗转相除算法，求它们的最小公倍数。

请编写函数fun，它的功能是：求任意两个正整数的最小公倍数和最大公约数，最小公倍数放在指针变量bei所指的变量中，最大公约数放在指针变量yue所指的变量中。

注意：部分源程序在文件PROG1.C中。请勿改动主函数main和其他函数中的任何内容，仅在函数fun的花括号中填入你编写的若干语句。

vOid fun(int m，int n，int*bei，int*yue)

{int s=l，i;

if(m＞n){s=m；m=n；n=S；}

for(i=2，s=1；i＜m i++)

if((m%i=0)&&(n%i=0))

{

}

*yue=s；

*bei=S*m*n；

}

main( )

{int a，b，beishu,yueshu；

chscr( )；

printf("please input a,b：")；scanf("%d，%d，"&a，&b)；

fun(a，b，&beishu,&yueshu)；

printf("a，b beishu：%d\n",beishu)；

printf("a，b yueshu：%d\n"，Yueshu)；

}

阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。

[说明]

下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：

(1)以n除m并令r为所得的余数；

(2)若r等于0，算法结束；n即为所求；

(3)将n和r分别赋给m和n，返回步骤(1)。

[流程图]

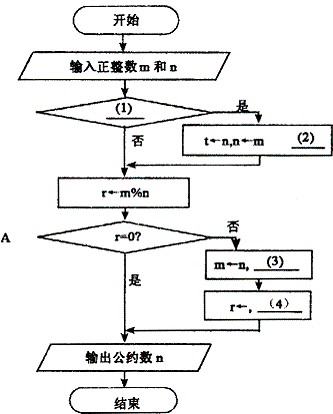
[问题1] 将流程图中的(1)～(4)处补充完整。

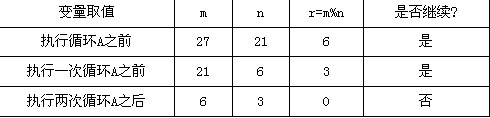
[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。

设M(m，n)是抛物线上的一点(m、n为正整数)，且它位于对称轴的右侧．若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数，求点M的坐标；

请补充main函数，该函数的功能是：输入两个正整数numl和num2，求这两个数的最大公约和最小公倍数。

例如，若输入的两个正整数为12，4，则它们的最大公约数为12，最小公倍数为4。

注意：部分源程序给出如下。

请勿改动main函数和其他函数中的任何内容，仅在main函数的横线上填人所编写的若干表达式或语句。

试题程序：

include<stdlib．h>

include<stdio．h>

void main

{

int a，b，numl，num2，t；

system("CLS")：

printf("\nInput two numbers：\n")；

scanf("%d，%d"，&numl，&num2)；

if(numl<num2)

{

a=num2；

b=num1：

}

else

{

a=num1；

b=num2；

}

while(【1】)

{

t=【2】

a=b；

b=t：

}

printf(“greatest common divisor：

%d\n"，a)；

printf("least common multiple：

%d\n"，【3】；

}

设M和N为正整数，且M>2，N>2，MN<2（M+N），满足上述条件的例(M,N)共有（）对。

A.3

B.5

C.6

D.7

请补充main函数，该函数的功能是：输入两个正整数m和n，求这两个数的最大公约和最小公倍数。

注意：部分源程序给出如下。

请勿改动主函数main和其他函数中的任何内容，仅在 main函数的横线上填入所编写的若干表达式或语句。

试题程序：

include ＜stdio.h＞

main ( )

{

int a, b, n, m, t;

clrscr ();

printf ("\nInput two numbers: \n");

scanf ("%d, %d", &n, &m);

if (n＜m)

{

a=m;

b=n;

}

else

{

a=n;

b=m;

}

while(【 】)

{

t=【 】

a=b;

b=t;

}

printf ("greatest con. non divisor:

%d\n", a);

printf ("least common multiple:

%d\n",【 】);

}

T(n)=O(f(n))中，函数O()的正确含义为

A.T(n)为f(n)的函数

B.T(n)为n的函数

C.存在足够大的正整数M，使得T(n)≤M×f(n)

D.存在足够大的正整数M，使得M×f(n)≤T(n)