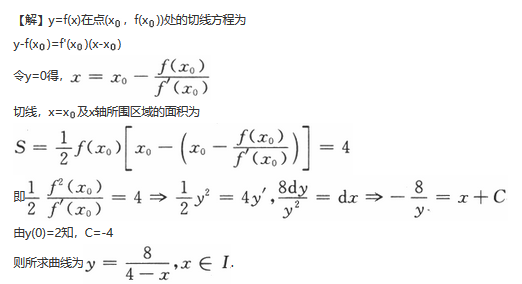违法和不良信息举报 联系客服
免费注册 登录

设f(x)，g(x)在x=x0处均不连续，则在x=x0处( )

题目
设f(x)，g(x)在x=x0处均不连续，则在x=x0处( )


A.f(x)+g(x)f(x)·g(X)均不连续

B.f(x)+g(x)不连续,f(x)·g(x)的连续性不确定

C.f(x)+g(x)的连续性不确定,f(x)·g(x)不连续

D.f(x)+g(x)f(x)·g(x)的连续性均不确定
如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

若函数f(x)在x0处连续,则f(x)在x0处极限存在。()

此题为判断题(对，错)。


参考答案：正确

第2题：

若函数f(x)在点x0间断，g(x)在点x0连续，则f(x)g(x)在点x0 ：
A.间断
B.连续
C.第一类间断
D.可能间断可能连续


答案：D
解析：
提示:通过举例来说明。连续的例题:设：x0=0，在x0=0处间断，g(x)=0，在x=0处连续，而f(x)?g(x)=0，在x0=0连续。
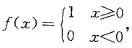间断的例题:设：x0=0，在x0=0处间断，g(x)=1，在x=0处连续，而f(x)?g(x)=0，在x0=0连续。
而

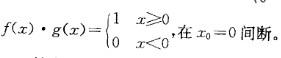
第3题：

以下结论正确的是()。

A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.

B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.

C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.

D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.


参考答案：C

第4题：

下列命题正确的是（）

A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
D.若函数f(x)在点x0处连续，则f'(x0)一定存在

答案：C
解析：
根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的．

第5题：

函数y=f(x) 在点x=x0处取得极小值，则必有：
A. f'(x0)=0
B.f''(x0)＞0
C. f'(x0)=0且f''(x0)＞0
D.f'(x0)=0或导数不存在


答案：D
解析：
提示：已知y=f(x)在x=x0处取得极小值，但在题中f(x)是否具有一阶、二阶导数，均未说明，从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况，如y= x 在x=0处导数不存在，但函数y= x 在x=0取得极小值。

第6题：

函数f（x）在点x＝x0处连续是f（x）在点x＝x0处可微的（　　）。

A．充分条件
B．充要条件
C．必要条件
D．无关条件

答案：C
解析：
可导等价于可微，可导必连续，而连续未必可导，如函数y＝|x|在x＝0处函数连续但不可导。因此可微是连续的充分条件，连续是可微的必要条件。

第7题：

函数y=f(x)在点x=x0处取得极小值，则必有：

A.f′(x0)=0
B.f′′(x0)＞0
C. f′(x0)=0 且 f(xo)＞0
D.f′(x0)=0 或导数不存在

答案：D
解析：
已知y=f(x)在x=x0处取得极小值，但在题中f(x)是否具有一阶、二阶导数，均未说明，从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况，如 ：y= x 在x=0处导数不存在，但函数y= x 在x=0取得极小值。

第8题：

设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。

A、0

B、π/2

C、锐角

D、钝角


参考答案：C

第9题：

若函数f (x)在点x0间断，g(x)在点x0连续，则f (x)g(x)在点x0:
(A)间断 (B)连续 (C)第一类间断（D)可能间断可能连续


答案：D
解析：
解：选D。
这道题可以用举例子的方法来判断。
f (x)g(x)=0在点处间断。

第10题：

设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.


答案：
解析：

更多相关问题
相关内容