第1题：
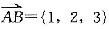为直线的方向向量，直线的对称式方程为
=
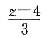
第2题：
式中t为时间，v0，g为常数，点的运动轨迹应为：
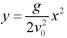，为抛物线第3题：
已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b>；0）交于A，B两点．
（I）求C的顶点到2的距离；
（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．
第4题：
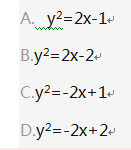
第5题：
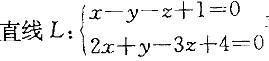平行的直线方程是：
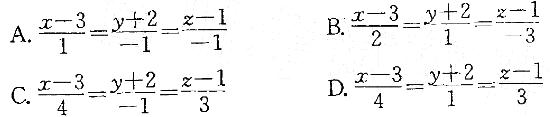
第6题：
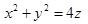
第7题：
平行的直线方程是：
第8题：
（2） 设点P是椭圆C的左准线与 x轴的交点，过点P的直线L与椭圆C相交于M.N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线L的斜率的取值范围。
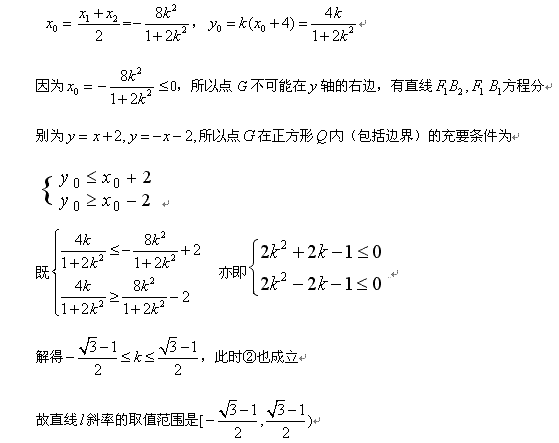
第9题：
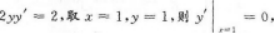
第10题：
