第1题:
设F(x)=P(X≤x)是连续型随机变量X的分布函数,则下列结论中不正确的是
A、F(x)是不增函数
B、0≤F(x)≤1
C、F(x)是右连续的
D、F(-∞)=0,F(+∞)=1
第2题:

第3题:
设f (x)=e5x,则f′(0)=_________.
第4题:

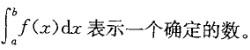
第5题:

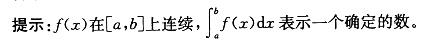
第6题:
设f(x)=(x-1)(x-2)(x-3),则方程f′(x)=0在(0,3)内的根的个数为(56)。
A.1
B.2
C.3
D.4
第7题:
第8题:
A、X=Y
B、X==Y
C、X<>Y
D、AT(X,Y)=0
第9题:
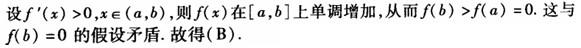
第10题: