第1题:
下列叙述中,正确的是()。
A.若线性回归相关系数r=1,则两个变量线性无关
B.若线性回归相关系数r>0,当x增加时,y值增加
C.当相关系数r=1时,所有的实验点都落在回归线上
D.当相关系数r=0时,可能两个变量间有某种曲线的趋势
第2题:
第3题:
下列关于相关系数r的数值范围的说法有误的是( )。 A.0.8<|r|<1为高度相关 B.当|r|=1时,表示两指标变量完全线性相关 C.当|r|=0时,表示两指标变量不存性相关 D.O<1,f≤0.3为低度相关
第4题:
第5题:

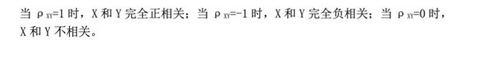
第6题:
A、当n<50,可查r界值表
B、以上均可
C、可用r检验
D、可用t检验
第7题:
第8题:
A、相关系数r反映变量间线性相关强度,是相关性的度量指标
B、相关系数r取值范围[-1,1]
C、关系数r的正负号能反映相关方向,大于零代表正相关,小于零代表负相关。
D、相关系数r大小可以反映相关程度,r越大则相关性越弱。
第9题:
第10题: