已知二次函数y1=x2-x-2和一次函数y2=x+1的两个交点分别为A(-1,0),B(3,4),当y1>y2时,自变量x的取值范围是( )
A.x<-1或x>3 B.-1<x<3 C.x<-1 D.x>3
第1题:
以下程序中,函数fun的功能是计算x2-2x+6,主函数中将调用fun函数计算,请填空。y1=(x+8)2-2(x+8)+6y2=sin2(x)-2sin(x)+6 #include "math.h"double fun(double x){ return();}main(){double x,y1,y2; printf("Enter x:"); scanf("%1f,&x); y1=fun(8+x); y2=fun(); printf("y1=%1f,y2=%1f\n",y1,y2);}
第2题:
●分别运行下列两段程序后,y1和y2的值是(39)。
程序段1:
#define f(x) x*x
floatX,y1;
X=2.0;
Y1=x/f(x);
程序段2:
#define f(x) (x*x)
floatx,y2;
X=2.0;
y2=x/f(x);,
( 39)A.y1=2.0,y2=0.5
B.y1=0.5,y2=2.0
C. y1=2.0,y2=1.0
D. y1=1.0,y2=2.0
第3题:
以下程序中,函数 fun 的功能是计算 x 2-2x+6 ,主函数中将调用 fun 函数计算:
y1=(x+8) 2-2 (x+8)+6
y2=sin 2(x)-2sin(x)+6
请填空。
#include "math.h"
double fun(double x){ return (x*x-2*x+6); }
main()
{ double x,y1,y2;
printf("Enter x:"); scanf("%lf",&x);
y1=fun( 【 11 】 );
y2=fun( 【 12 】 );
printf("y1=%lf,y2=%lf\n",y1,y2);
}
第4题:
第5题:
阅读以下说明和c++代码,将应填入(n)处的字句写在对应栏内。
【说明】
现要编写一个画矩形的程序,目前有两个画图程序:DP1和DP2,DP1用函数draw_a_line(x1, y1,x2,y2)画一条直线,DF2则用drawline(x1,x2,y1,y2)画一条直线。当实例画矩形时,确定使用DP1还是DP2。为了适应变化,包括“不同类型的形状”和“不同类型的画图程序”,将抽象部分与实现部分分离,使它们可以独立地变化。这里,“抽象部分”对应“形状”,“实现 部分”对应“画图”,与一般的接口(抽象方法)与具体实现不同。这种应用称为Bridge(桥接)模式。图9-7显示了各个类间的关系。
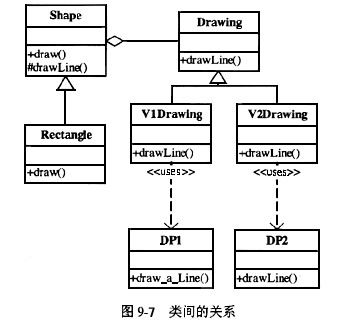
这样,系统始终只处理3个对象:Shape对象、Drawing对象、DP1或DP2对象。以下是 C++语言实现,能够正确编译通过。
【C++代码】
class DP1{
public:
static void draw_a_line(double x1, double y1,double x2, double y2){
//省略具体实现
}
);
class DP2{
public:
static void drawline(double x1, double x2,double y1, double y2){
//省略具体实现
}
};
class Drawing{
public:
(1) void drawLine(double x1,double y1,double x2,double y2)=0;
};
class V1Drawing:public Drawing{
public:
void drawLine(double x1, double y1,double x2, double y2){
DP1::draw_a_line(x1,y1,x2,y2);
}
};
class V2Drawing:public Drawing{
public:
void drawLine(double x1, double y1, double x2, double y2){
(2);
}
};
class Shape{
private:
(3) _dp;
public:
Shape(Drawing *dp);
virtual void draw()=0;
void drawLine(double x1, double y1, double x2, double y2);
};
Shape::Shape(Drawing *dp)
{
_dp = dp;
}
void Shape::drawLine(double x1, double y1, double x2, double y2)
{ //画一条直线
(4);
}
class Rectangle: public Shape{
private:
double _x1,_y1,_x2,_y2;
public:
Rectangle(Drawing *dp, double x1, double y1,
double x2, double y2);
void draw();
};
Rectangle::Rectangle(Drawing *dp, double x1, double y1, double x2, double y2)
:(5)
{
_x1=x1;_y1=y1;_x2=x2;_y2=y2;
}
void Rectangle::draw()
{
//省略具体实现
}
第6题:
在由两个不同组别消费者组成的市场1和市场2上,产量分别为Y1和Y2,消费者反需求函数为P1(Y1)和P2(Y2),用C(Y1+Y2)表示生产的成本,则在三级价格歧视下,厂商在两个市场上总产量分割满足什么条件时,以实现利润最大化。()
A.MC(Y1+Y2)=MR1(Y1)=MR2(Y2
B.MR2(Y2)>MC(Y1+Y2)=MR1(Y1)
C.MR1(Y1)>MC(Y1+Y2)=MR2(Y2)
D.MR1(Y1)=MR2(Y2)=MC(Y1+Y2)
第7题:
以下程序中,函数fun的功能是计算x2(上标)-2x+6,主函数中将调用fun函数计算:
y1=(x+8)2(上标)-2(x+8)+6
y2=sin2(上标)(x)-2sin(x)+6
请填空。
include "math.h"
double fun(double x){ return (x*x-2*x+6);}
main()
{ double x,y1,y2;
printf("Enter x:"); scanf("%1f",&x);
y1=fim([ ]);
y2=run([ ]);
printf("y1=%1f,y2=%1f\n",y1,y2);
}
第8题:
A、{x=1,y={y1=10,y2=3}}
B、{x=1,y={y1=2,y2=3}}
C、{'x':1,'y':{'y1':10,'y2':3}}
D、{'x':1,'y':{'y1':2,'y2':3}}
第9题:
程序段如下,当发生Form_Click事件时,窗体上输出的结果是( )。 Option Explicit Private x As Integer Public y As Integer Sub Test() Dim y as integer x=2:y=2 Print"x1=";x;"y1=";y End Sub Private Sub Form_Click() x=1:y=1 Test Print "X2=";x;"y2=";y End Sub
A.x1=2 y1=2 x2=2 y2=1
B.x1=2 y1=2 x2=2 y2=2
C.x1=2 y1=1 x2=2 y2=2
D.x1=2 y1=1 x2=2 y2=1
第10题: