递归算法题1一个整数，大于0，不用循环和本地变量，按照n，2n，4n，8n 的顺序递增，当值大于5000 时，把值按照指定顺序输出来。

题目

递归算法题1

一个整数，大于0，不用循环和本地变量，按照n，2n，4n，8n 的顺序递增，当

值大于5000 时，把值按照指定顺序输出来。

如果没有搜索结果或未解决您的问题，请直接联系老师获取答案。

相似问题和答案

第1题：

【单选题】设有一个递归算法如下

A．int fact(int n) { //n大于等于0

B．if(n＜=0) return 1;

C．else return n*fact(n-1); }

D．算fact(n)需要调用该函数的次数为（）。

E．n+1

F．n-1

G．n

H．n+2

D。参考解析：需计算18次函数。

第2题：

5、设有一个递归算法如下 int fact（int n) { //n大于等于0 if（n＜=0) return 1; else return n*fact（n-1); } 则计算fact（n)需要调用该函数的次数为（）。

A．n-1

B．n

C．n+1

D．n+2

t fact(int n) { //n大于等于0

第3题：

第一题阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n，(x+1)n可展开为

问题：1.1 【流程图】

注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1。
格式为：循环控制变量=初值，终值，递增值。

答案：

解析：

（1）2，n，1
（2）A[k]
（3）k-1，1，-1
（4）A[i]+A[i-1]
（5）A[i]
【解析】

（1）（3）空为填写循环初值终值和递增值，题目中给出的格式为循环控制变量=初值，终值，递增值。按照题意，实质为求杨辉三角。如下图：

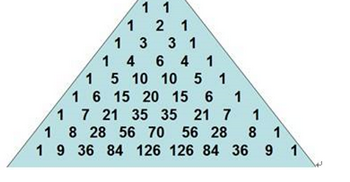
第4题：

某大型整数矩阵用二维整数组 G[1：2M ，l：2N]表示，其中M和N是较大的整数，而且每行从左到右都己是递增排序，每到从上到下也都己是递增排序。元素G[M，N]将该矩阵划分为四个子矩阵A[1：M，1：N]，B[1:M，(N+1):2N]，C[(M+1）:2M，1:N ]，D[(M+1）:2M，(N+1):2N]。如果某个整数E大于A[M，N]，则E（）。

A.只可能在子矩阵A中B.只可能在子矩阵B或C中C.只可能在子矩阵B、C或D中D.只可能在子矩阵D中

正确答案：C

第5题：

在PCR反应中，经过n次循环，理论上DNA链的数目扩增了多少倍

A、n倍

B、2n倍

C、4n倍

D、8n倍

E、16n倍

参考答案：B

第6题：

设变量x是一个整型变量，如果sgn（x）的值为1，则X的值是（）。

A.1

B.大于0的整数

C.0

D.小于0的整数

正确答案：B
B．【解析】本题考查VBA中判断符号函数的知识。Sgn0函数是一个判断符号的函数，其参数为数值型的值，若参数小于0，则函数返回一1；若参数等于0，则函数返回0；若参数大于0，则函数返回l。

第7题：

设有一个递归算法如下int fact(intn){//n 大于等于0 if(n＜=0)return 1； else return n* fact(n--)； }则计算fact(n)需要调用该函数的次数为(30)次。

A．n

B．n+1

C．n+2

D．n-1

正确答案：B
解析：n--为先使用后自减所以调用n-1次时的值为0终止调用

第8题：

设有一个递归算法如下intfact(intn){／／n大于等于0if(n<=0)return1;elsereturnn*fact(n－1);}则计算fact(n)需要调用该函数的次数为()。

A.n+1

B、n-1

C、n

D、n+2

参考答案：A
解释：特殊值法。设n=0，易知仅调用一次fact(n)函数，故选A。

第9题：

设变量x是一个整型变量，如果Sgn(x)的值为1，则x的值是( )。

A．1

B．大于0的整数

C．0

D．小于0的整数

正确答案：B
解析：本题考查VBA中判断符号函数的知识。Sgn()函数是一个判断符号的函数，其参数为数值型的值，若参数小于0，则函数返回-1：若参数等于0，则函数返回0；若参数大于0，则函数返回1。

递归算法题1一个整数,大于0,不用循环和本地变量,按照n,2n,4n,8n 的顺序递增,当值大于5000 时,

题目

相似问题和答案

相关内容