第1题：
一个含有n个顶点和e条边的简单无向图，在其邻接矩阵存储结构中共有______个零元素。
A．e
B．2e
C．n2-e
D．n2-2e
第2题：
有n个顶点的无向图, 采用邻接矩阵表示, 图中的边数等于邻接矩阵中非零元素之和的一半。()
第3题：
●试题六
阅读以下说明和C++代码，将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
本题将有向网(带权有向图)定义为类AdjacencyWDigraph。类中的数据成员n表示有向网中的顶点数;a为带权邻接矩阵，用于存储有向网中每一对顶点间弧上的权值;c为二维数组，存储有向网中每一对顶点间的最短路径长度;kay为二维数组，存储最短路径，kay［i］［j］=k表示顶点i 到达顶点j的最短路径必须经过顶点k。类中的主要成员函数有：
Input():输入有向网的顶点数、各条弧及权值，建立带权领接矩阵a。若顶点i到顶点j有弧，则a［i］［j］取弧上的权值，否则a［i］［j］的值取NoEdge。
AllPairs();用弗洛伊德(Floyd)算法求有向网中每一对顶点间的最短路径长度。
OutShortestPath(int i,int j):计算顶点i到顶点j的最短路径。
outputPath(int i,int j):输出顶点i到顶点j的最短路径上的顶点。
Floyd算法的基本思想是递推地产生一个矩阵序列C0,C1，C2，…，Cn,其中C0是已知的带权邻接矩阵，a,Ck(i,j)(0≤i,j＜n)表示从顶点i到顶点j的中间顶点序号不大于k 的最短路径长度。如果i到j的路径没有中间顶点，则对于0≤k＜n,有Ck(i,j)=C0(i,j)=a［i］［j］。递推地产生C1，C2，…，Cn的过程就是逐步将可能是最短路径上的顶点作为路径上的中间顶点进行试探，直到为全部路径都找遍了所有可能成为最短路径上的中间顶点，所有的最短路径也就全部求出，算法就此结束。
【C++代码】
#include<iostream．h>
＃define NoEdge 10000 //当两个顶点之间没有边相连时，在邻接矩阵中用NoEdge表示
void Make2DArray(int * * &x,int rows,int cols);
class AdjacencyWDigraph{
private
int n;//有向网中的顶点数目
int**a;//存储顶点间弧上的权值
int**c;//存储计算出的最短路径长度
int**kay;//存储求出的最短路径
pubic:
int Vertices()const {return n;}
void AllPairs();
void Input();//输入有向网的顶点数、各条弧及权值，建立邻接矩阵a
void OutShortestPath(int i,int j);//计算顶点i到j的最短路径(试卷中未列出)
~AdjacencyWDigraph();//析构函数(试卷中未列出)
private:
void outputPath(int i,int j);
};
void AdjacencyWDigraph::AllPairs()
{int i,j,k,t1,t2,t3;
for(i=1;i＜=n;k++)
for(j=1;j＜=n;++j)
{c［i］［j］= (1) ;kay［i］［j］=0;}
for(k=1;k＜=n;k++)
for(i=1;i＜=n;i++){
if(i==k) continue;
t1=c［i］［k］;
for(j=1;j＜=n;j++){
if(j==k||j==i)continue;
t2=c［k］［j］;t3=c［i］［j］;
if(t1!=NoEdge && t2!=NoEdge &&(t3==NoEdge||t1+t2＜t3))
{c［i］［j］= (2) ；kay［i］［j］= (3) ;}
}//for
}//for
}
void AdjacencyWDigraph:: outputPath(int i,int j)
{//输出顶点i到j的最短路径上的顶点
if(i==j)return;
if(kay［i］［j］==0)cout＜＜j＜＜′′;
else { outputPath(i, (4) ); outputPath( (5) );}
}
void Adjacency WDigraph::Input()
{int i,j,u,v,w,E;
cout＜＜″输入网中顶点个数：″;cin＞＞n;
cout＜＜″输入网中弧的个数:″;cin＞＞E;
Make2DArray(a,n+1,n+1);
for(i=1;i＜=n;i++)
for(j=1;j＜=n;j++)a［i］［j］=NoEdge;
for(i=1;i＜=n;i++)a［i］［i］=0;
Make2DArray(c,n+1,n+1);
Make2DArray(kay,n+1,n+1);
for(i=1;i＜=E;i++){
cout＜＜″输入弧的信息(起点终点权值)：″；cin＞＞u＞＞v＞＞w;a［u］［v］=w;
}
}
void Make2DArray(int**&x,int rows,int cols)
{int i,j;
x=new int*［rows+1］;
for(i=0;i＜rows+1;i++)x［i］=new int ［cols+1］;
for(i=1;i＜=rows;i++)
for(j=1;j＜=cols;j++＝x［i］［j］=0;
}
●试题六
【答案】（1）a［i］［j］（2）t1+t2,其中t1可以写成c［i］［k］,t2可以写成c［k］［j］
（3）k（4）kay［i］［j］（5）kay［i］［j］,j
【解析】（1）此处的双层循环的作用是给数组c赋初值。即把最初的i号结点到j号结点的路径长度存入c。由题目中已经有说明："Input（）；输入有向图的顶点数、各条弧及权值，建立带权邻近矩阵a。若顶点i到顶点j有弧，则a［i］［j］取弧上的权值，否则a［i］［j］的值取NoEdge。"所以应填a［i］［j］。（2）首先应该说明的是此处的三层循环所完成的功能是用递推的方式，在i号结点和j号结点中插入一个k号结点，然后比较c［i］［j］与c［i］［k］＋c［k］［j］，如果c［i］［k］＋c［k］［j］小于c［i］［j］，则用 c［i］［k］+c［k］［j］代替 c［i］［j］。这里用到的原则就是： c［i］［k］，c［k］［j］分别是i到k，k到j的最短路径，若i到j要经过k，则 c［i］［k］+c［k］就是i到j过结点k的最短路径。（3）由于题目中提到"kay为二维数组，存储最短路径，kay［i］［j］=k表示顶点i到达顶点j的最短路径必须经过顶点k。"所以，应填k。（5）此处用到了程序的递归，其实这个过程很好理解，也就是判断当中间结点为0，表示i，j直接为最短路径，则直接打印即可。如果有中间结点k，则先打印从i到k的路径，再打印从k到j的路径。此处的中间结点存在kay［i］［j］里，所以（4）填kay［i］［j］。
第4题：
若采用邻接矩阵来存储简单有向图，则其某一个顶点i的人度等于该矩阵______。
A．第i行中值为1的元素个数
B．所有值为1的元素总数
C．第i行及第i列中值为1的元素总个数
D．第i列中值为1的元素个数
第5题：
用相邻矩阵A表示图，判定任意两个顶点Vi和Vi，之间都有长度为m的路径相连，则只要检查(40)的第i行第j列的元素是否为0即可。
从邻接矩阵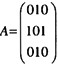
可以看出，该图共有(41)个顶点。如果是有向图，该图有(42)条弧；如果是无向图，则共有(43)条边。
A．mA
B．A
C．Am
D．Am-1
第6题：
若采用邻接矩阵来存储简单有向图，则其某一个顶点i的入度等于该矩阵______。
A．第i行中值为1的元素个数
B．所有值为1的元素总数
C．第i行及第i列中值为1的元素总个数
D．第i列中值为1的元素个数
第7题：
第8题：
设一个包含N个顶点、E条边的简单有向图采用邻接矩阵存储结构(矩阵元素A[i][j]等于1/0分别表示顶点i与顶点j之间有/无弧)，则该矩阵的元素数目为(58)，其中非零元素数目为(59)。
A．E2
B．N2
C．N2-E2
D．N22+E2
第9题：
A、计算邻接矩阵中第i行的元素之和
B、计算邻接矩阵中第i列的元素之和
C、计算邻接矩阵中第i行的非零元个数
D、计算邻接矩阵中第i列的非零元个数
第10题：
●设一个包含N 个顶点、E 条边的简单无向图采用邻接矩阵存储结构（矩阵元素 A[i][j]等于1/0 分别表示顶点i与顶点 j 之间有／无边），则该矩阵中的非零元素数目为 (60)。
(60)
A．N
B．E
C．2E
D．N+E