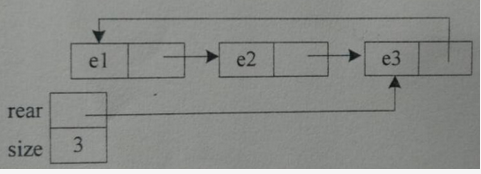
第1题:
阅读以下说明和C语言函数,将应填入(n)处的字句写在答题纸的对应栏内。
[说明]
求树的宽度,所谓宽度是指在二叉树的各层上,具有结点数最多的那一层的结点总数。本算法是按层次遍历二叉树,采用一个队列q,让根结点入队列,若有左右子树,则左右子树根结点入队列,如此反复,直到队列为空。
[函数]
int Width ( BinTree *T
{
int front=-1, rear=-1; /*队列初始化*/
int flag=0, count=0, p; /*p用于指向树中层的最右边的结点, flag 记录层中结点数的最大值*/
if ( T!=Null)
{
rear++;
(1);
flag=1;
p=rear;
}
while ((2))
{
front++;
T=q [front]];
if (T->lchild!=Null )
{
roar+-+;
(3);
count++;
}
if ( T->rchild!=Null )
{
rear++; q[rear]=T->rchild;
(4);
}
if (front==p ) // 当前层已遍历完毕
{
if((5))
flag=count;
count=0;
p=rear, //p 指向下一层最右边的结点
}
}
return ( flag );
}
第2题:
阅读下列函数说明和Java代码,将应填入(n)处的字句写在对应栏内。
【说明】
类Queue表示队列,类中的方法如下表所示。

类Node表示队列中的元素;类EmptyQueueException给出了队列操作中的异常处理操作。
public class TestMain { //主类
public static viod main (String args[]){
Queue q=new Queue();
q.enqueue("first!");
q.enqueue("second!");
q.enqueue("third!");
(1) {
while(true)
System.out.println(q.dequeue());
}
catch( (2) ){ }
}
public class Queue { //队列
Node m_FirstNode;
public Queue(){m_FirstNode=null;}
public boolean isEmpty(){
if(m_FirstNode==null)return true;
else return false;
}
public viod enqueue(Object newNode) { //入队操作
Node next=m_FirstNode;
if(next==null)m_FirstNode=new Node(newNode);
else{
while(next.getNext()!=null)next=next.getNext();
next.setNext(new node(newNode));
}
}
public Object dequeue() (3) { //出队操作
Object node;
if (isEempty())
(4); //队列为空, 抛出异常
else{
node=m_FirstNode.getObject();
m_FirstNode=m_FirstNode.getNext();
return node;
}
}
}
public class Node{ //队列中的元素
Object m_Data;
Node m_Next;
public Node(Object data) {m_Data=data; m_Next=null;}
public Node(Object data, Node next) {m_Data=data; m_Next=-next;}
public void setObject(Object data) {m_Data=data;}
public Object getObject(Object data) {return m_data;}
public void setNext(Node next) {m_Next=next;}
public Node getNext() {return m_Next;}
}
public class EmptyQueueException extends (5) { //异常处理类
public EmptyQueueException() {
System.out.println("队列已空! ");
}
}
第3题:
●试题四
阅读下列函数说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明4.1】
假设两个队列共享一个循环向量空间(如图1-2所示),其类型Queue2定义如下:
typedef struct{
DateType data [MaxSize];
int front[2],rear[2];
}Queue2;
对于i=0或1,front[i]和rear[i]分别为第i个队列的头指针和尾指针。函数EnQueue(Queue2*Q,int i,DateType x)的功能是实现第i个队列的入队操作。
【函数4.1】
int EnQueue(Queue2*Q,int i,DateType x)
{∥若第i个队列不满,则元素x入队列,并返回1;否则,返回0
if(i<0‖i>1)return 0;
if(Q->rear[i]==Q->front[ (1) ]
return 0;
Q->data[ (2) ]=x;
Q->rear[i]=[ (3) ];
return 1;
}
【说明4.2】
函数BTreeEqual(BinTreeNode*T1,BinTreeNode*T2)的功能是递归法判断两棵二叉树是否相等,若相等则返回1,否则返回0。函数中参数T1和T2分别为指向这两棵二叉树根结点的指针。当两棵树的结构完全相同,并且对应结点的值也相同时才被认为相等。
已知二叉树中的结点类型BinTreeNode定义为:
struct BinTreeNode{
char data;
BinTreeNode*left,*right;
};
其中data为结点值域,left和right分别为指向左、右子女结点的指针域,
【函数4.2】
int BTreeEqual(BinTreeNode*T1,BinTreeNode*T2)
{
if(T1==NULL && T2==NULL)return 1;∥若两棵树均为空,则相等
else if( (4) )return 0;∥若一棵为空一棵不为空,则不等
else if( (5) )return 1;∥若根结点值相等并且左、右子树
∥也相等,则两棵树相等,否则不等
else return 0;
}
●试题四
【答案】(1)(i+1)%2(或1-i)(2)Q->rear[i](3)(Q->rear[i]++)%Maxsize
(4)Tl==NULL‖T2==NULL(5)Tl->data==T2->data && BTreeEqual(T1->left,T2->left) && BTreeEqual(T1->right,T2->right)
【解析】这一题共有两个函数,第一个函数是一个循环共享队列入队的的问题,第二个函数是用递归法判断两棵二叉树是否相等的问题。
先分析第一个函数。(1)空所在if语句是判断是否能入队,当队列0入队时,如果队列0队尾指针与队列1队头指针相等时,说明队列0无法入队;当队列1入队时,如果队列1队尾指针与队列0队头指针相等时,说明队列1无法入队。因此(1)空处应填写"(i+1)%2"或"1-i"。(2)、(3)空是入队操作,其操作步骤是先将元素x插入队列i队尾所指的位置,再将队尾"加1"。因此(2)空处应填写"Q->rear[i]";由于是一个循环队列,(3)空处应填写"(Q->rear[i]+1)%Maxsize"。
再分析第二个函数。这一题比较简单,只需将程序注释转换成C语言即可得到答案。(4)空所处理的是若一棵为空,而一棵不为空则不相等,显然(4)空应填入"T1==NULL‖T2==NULL"。(5)空处是一个递归调用,处理若根结点值相等并且左、右子树也相等,则两棵树相等,因此(5)空应填入"T1->data==T2->data && BTreeEqual(T1->left,T2->left)&&BTreeEqua1(T1->right,T2->right)"及其等价形式。
第4题:
阅读以下说明和C语言函数,将应填入(n)。
【说明】
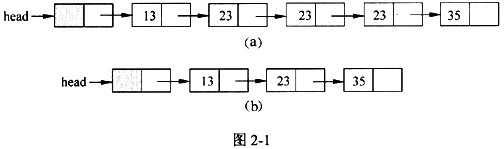
已知包含头结点(不存储元素)的单链表的元素已经按照非递减方式排序,函数 compress(NODE*head)的功能是去掉其中重复的元素,使得链表中的元素互不相同。
处理过程中,当元素重复出现时,保留元素第一次出现所在的结点。
图2-1(a)、(b)是经函数compress()处理前后的链表结构示例图。
链表的结点类型定义如下:
typedef struct Node{
int data;
struct Node *next;
}NODE;
【C语言函数】
void compress(NODE *head)
{ NODE *ptr,*q;
ptr= (1); /*取得第一个元素结点的指针*/
while( (2)&& ptr->next) {
q=ptr->next;
while(q&&(3)) { /*处理重复元素*/
(4)q->next;
free(q);
q=ptr->next;
}
(5) ptr->next;
}/*end of while */
}/*end of compress*/
第5题:
阅读下列说明和C代码,将应填入(n)处的字句写在对应栏内。
【说明】
本题给出四个函数,它们的功能分别是:
1.int push(PNODE*top,int e)是进栈函数,形参top是栈顶指针的指针,形参e是入栈元素。
2.int pop(PNODE*top,int*e)是出栈函数,形参top是栈顶指针的指针,形参e作为返回出栈元素使用。
3.int enQueue(PNODE*tail,int e)是入队函数,形参tail是队尾指针的指针,形参e是入队元素。
4.int deQueue(PNODE*tail,int*e)是出队函数,形参tail是队尾指针的指针,形参e作为返回出队元素使用。
以上四个函数中,返回值为。表示操作成功,返回值为-1表示操作失败。
栈是用链表实现的;队是用带有辅助结点(头结点)的单向循环链表实现的。两种链表的结点类型均为:
typedef struct node {
int value;
struct node * next;
} NODE, * PNODE;
【函数1】
int push(PNOOE * top,int e)
{
PNODE p = (PNODE) malloc (sizeof (NODE));
if (! p) return-1;
p->value=e;
(1);
*top=p;
return 0;
}
【函数2】
int pop (PNODE * top,int * e)
{
PNODE p = * top;
if(p == NULL) return-1;
* e = p->value;
(2);
free(p);
return 0;
}
【函数3】
int enQueue (PNODE * tail,int e)
{ PNODE p,t;
t= *tail;
p = (PNODE) malloc(sizeof(NODE));
if(!p) return-1;
p->value=e;
p->next=t->next;
(3);
* tail = p;
return 0;
}
【函数4】
int deQueue(PNODE * tail,int * e)
{ PNODE p,q;
if(( * tail)->next == * tail) return-1;
p= (* tail)->next;
q = p ->next;
* e =q ->value;
(4)=q->next;
if(,tail==q) (5);
free(q);
return 0;
}
第6题:
阅读下列函举说明和C代码,将应填入(n)处的字句写在对应栏内。
【说明4.1】
假设两个队列共享一个循环向量空间(如图1-2所示),其类型Queue2定义如下:
typedef struct {
DateType data [MaxSize];
int front[2],rear[2];
}Queue2;
对于i=0或1,front[i]和rear[i]分别为第i个队列的头指针和尾指针。函数.EnQueue (Queue2*Q,int i,DaleType x)的功能是实现第i个队列的入队操作。
【函数4.1】
int EnQueue(Queue2 * Q, int i, DateType x)
{ /*若第i个队列不满,则元素x入队列,并返回1;否则,返回0*/
if(i<0‖i>1) return 0;
if(Q->rear[i]==Q->front[(1)]
return 0;
Q->data[(2)]=x;
Q->rear[i]=[(3)];
return 1;
}
【说明4.2】
函数BTreeEqual(BinTreeNode*T1,BinTtneNode*T2)的功能是递归法判断两棵二叉树是否相等,若相等则返回1,否则返回0。函数中参数T1和T2分别为指向这两棵二叉树根结点的指针。当两棵树的结构完全相同,并且对应结点的值也相同时,才被认为相等。
已知二叉树中的结点类型BinTreeNode定义为:
struct BinTreeNode {
char data;
BinTreeNode * left, * right;
};
其中dau为结点值域,leR和risht分别为指向左、右子女结点的指针域,
【函数4.2】
int BTreeEqual(BinTreeNode * T1, BinTreeNode * T2)
{
if(Ti == NULL && T2 == NULL)return 1 /*若两棵树均为空,则相等*/
else if((4))return 0; /*若一棵为空一棵不为空,则不等*/
else if((5)) return 1; /*若根结点值相等并且左、右子树*/
/*也相等,则两棵树相等,否则不等*/
else return 0;
}
第7题:
阅读下列函数说明和C函数,将应填入(n)处的字句写在对应栏内。
[说明]
循环队列的类型定义如下(其中队列元素的数据类型为datatype):
typedef struct{
datatype data[MAXSIZE]; /*数据的存储区*/
int front,rear; /*队首、队尾指针*/
int num; /*队列中元素的个数*/
}c _ SeQueue; /*循环队*/
下面函数及其功能说明如下:
(1) c_SeQueue* Init_SeQueue():新建队列;
(2) int ln_SeQueue( c_SeQueue *q, datatype x):将元素x插入队列q,若成功返回1否则返回0;
(3) int Out_SeQueue (c_SeQueue *q, datatype *x):取出队列q队首位置的元素,若成功返回1否则返回0。
[函数]
c_SeQueue* Init_SeQueue()
{ q=malloc(sizeof(c_SeQueue));
q->front=q->rear=MAXSIZE-1;
(1);
return q;
}
int In_SeQueue( c_SeQueue *q, datatype x)
{ if(q->num= =MAXSIZE) return 0; /*队满不能入队*/
else {
q->rear=(2);
q->data[q->rear]=x;
(3);
return 1; /*入队完成*/
}
}
int Out_SeQueue( c_SeQueue *q, datatype *x)
{ if (q->num= =0) return 0; /*队空不能出队*/
else{
*x=(4); /*读出队首元素*/
q->front=(5);
q->num- -;
return 1; /*出队完成*/
}
}
第8题:
●试题三
阅读下列说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
本题给出四个函数,它们的功能分别是:
1.int push(PNODE *top,int e)是进栈函数,形参top是栈顶指针的指针,形参e是入栈元素。
2.int pop(PNODE *top,int *e)是出栈函数,形参top是栈顶指针的指针,形参e作为返回出栈元素使用。
3.int enQueue(PNODE *tail,int e)是入队函数,形参tail是队尾指针的指针,形参e是入队元素。
4.int deQueue(PNODE *tail,int *e)是出队函数,形参tail是队尾指针的指针,形参e作为返回出队元素使用。
以上四个函数中,返回值为0表示操作成功,返回值为-1表示操作失败。
栈是用链表实现的;队是用带有辅助结点(头结点)的单向循环链表实现的。两种链表的结点类型均为:
typedef struct node{
int value;
struct node *next;
}NODE,*PNODE;
【函数1】
int push(PNODE *top,int e)
{
PNODE p=(PNODE)malloc (sizeof(NODE));
if (!p) return-1;
p-> value =e;
(1) ;.
*top=p;
return 0;
}
【函数2】
int pop (PNODE *top,int *e)
{
PNODE p=*top;
if(p==NULL)return-1;
*e=p->value;
(2) ;
free(p);
return 0;
}
【函数3】
int enQueue (PNODE *tail,int e)
{PNODE p,t;
t=*tail;
p=(PNODE)malloc(sizeof(NODE));
if(!p)return-l;
p->value=e;
p->next=t->next;
(3) ;
*tail=p;
return 0;
}
【函数4】
int deQueue(PNODE *tail,int *e)
{PNODE p,q;
if((*tail)->next==*tail)return -1;
p=(*tail)->next;
q=p->next;
*e=q->value;
(4) =q->next;
if(*tail==q) (5) ;
free(q);
return 0;
}
●试题三
【答案】(1)p->next=*top(2)*top=p->next或*top=(*top)->next
(3)t->next=p或(*tail)->next=p(4)p->next或(*tail)->next->next
(5)*tail=p或*tail=(*tail)->next
【解析】(1)插入结点p后,p应当指向插入前头结点,所以填入p->next=*top。(2)出栈后,头指针应指向它的下一结点,所以填入*top=p->next或*top=(*top)->next。(3)入队时,需要将结点插入队尾,所以应当填入(*tail)->next=p或t->next=p(t也指向尾结点)。(4)出队时,需要删除队头结点,通过(*tail)->next可以得到对队头结点的引用。(4)处是正常删除队头结点的情况,空格处应填入头结点指向下一结点的指针,即p->next或(*tail)->next->next。(5)处是需要考虑的特殊情况,即队列中最后一个元素出队后,要更新队尾指针,即填入*tail=p或*tail=(*tail)->next。
第9题:
阅读下列说明和C函数,将应填入(n)处的字句写在对应栏内。
【说明】
已知集合A和B的元素分别用不含头结点的单链表存储,函数Difference()用于求解集合A与B的差集,并将结果保存在集合A的单链表中。例如,若集合A={5,10, 20,15,25,30},集合B={5,15,35,25},如图(a)所示,运算完成后的结果如图(b)所示。

链表结点的结构类型定义如下:
typedef struct Node{
ElemType elem;
struct Node *next;
}NodeType;
【C函数】
void Difference(NodeType **LA,NodeType *LB)
{
NodeType *pa, *pb, *pre, *q;
pre=NULL;
(1);
while (pa) {
pb=LB;
while((2))
pb=pb->next;
if((3)) {
if(!pre)
*LA=(4);
else
(5)=pa->next;
q = pa;
pa=pa->next;
free(q);
}
else {
(6);
pa=pa->next;
}
}
}
第10题:
阅读下列函数说明和C函数,将应填入(n)处的字句写对应栏内。
[说明]
二叉树的二叉链表存储结构描述如下:
typedef struct BiTNode
{ datatype data;
struct BiTNode *lchild, * rchild; /*左右孩子指针*/
}BiTNode,* BiTree;
对二叉树进行层次遍历时,可设置一个队列结构,遍历从二叉树的根结点开始,首先将根结点指针入队列,然后从队首取出一个元素,执行下面两个操作:
(1) 访问该元素所指结点;
(2) 若该元素所指结点的左、右孩子结点非空,则将该元素所指结点的左孩子指针和右孩子指针顺序入队。
此过程不断进行,当队列为空时,二叉树的层次遍历结束。
下面的函数实现了这一遍历算法,其中Visit(datatype a)函数实现了对结点数据域的访问,数组queue[MAXNODE]用以实现队列的功能,变量front和rear分别表示当前队首元素和队尾元素在数组中的位置。
[函数]
void LevelOrder(BiTree bt) /*层次遍历二叉树bt*/
{ BiTree Queue[MAXNODE];
int front,rear;
if(bt= =NULL)return;
front=-1;
rear=0;
queue[rear]=(1);
while(front (2) ){
(3);
Visit(queue[front]->data); /*访问队首结点的数据域*/
if(queue[front]—>lchild!:NULL)
{ rear++;
queue[rear]=(4);
}
if(queue[front]->rchild! =NULL)
{ rear++;
queue[rear]=(5);
}
}
}