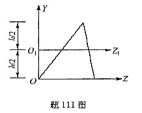
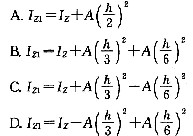
第1题:
第2题:
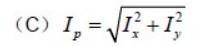


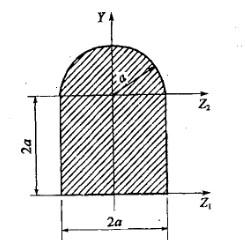
第3题:
A.截面面积
B.截面抵抗矩
C.惯性矩
D.面积矩
第4题:



第5题:
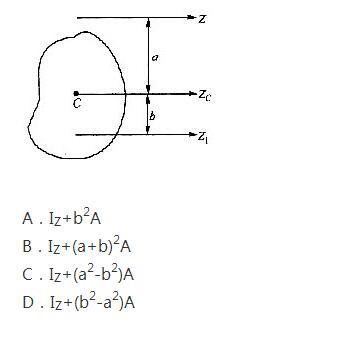
第6题:
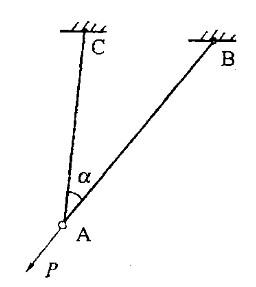
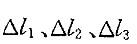 分别代表杆①、②、③的轴力和伸长,用表示点A的水平位移和竖直位移,则下列结论中正确的是:
分别代表杆①、②、③的轴力和伸长,用表示点A的水平位移和竖直位移,则下列结论中正确的是:
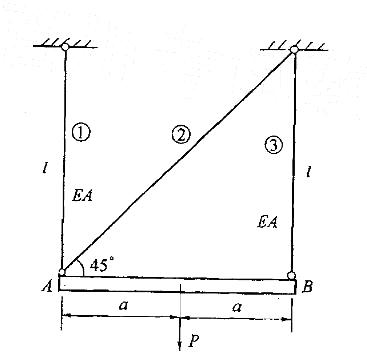
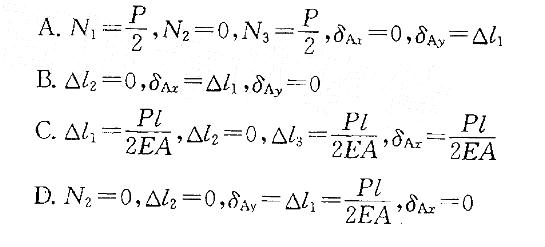
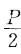 ,N2=0,N3=
,N2=0,N3=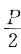 ;再用胡克定律可求出
;再用胡克定律可求出 =
= ,
, =0,
=0,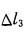 =
= ;由于A点受力变形后依然要连接杆①和杆②,故可用切线代替圆弧的办法求出A的水平位移。
;由于A点受力变形后依然要连接杆①和杆②,故可用切线代替圆弧的办法求出A的水平位移。第7题:

 求得。
求得。


第8题:
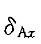 ,节点A的竖直位移为
,节点A的竖直位移为 ,则下列结论中正确的是:
,则下列结论中正确的是:
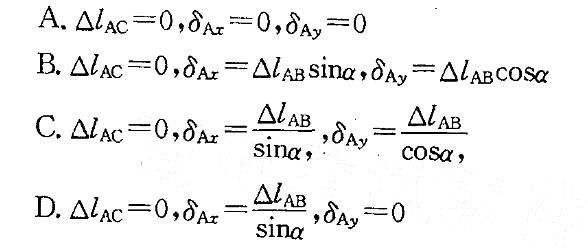
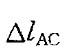 = 0,
= 0, 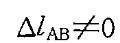 ,再用切线代替圆弧的方法求出变形后A点的位置,可以得出结论D是正确的。
,再用切线代替圆弧的方法求出变形后A点的位置,可以得出结论D是正确的。第9题:


第10题:
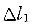 ,杆②的伸长量为
,杆②的伸长量为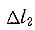 ,则下列结论中正确的是:
,则下列结论中正确的是:

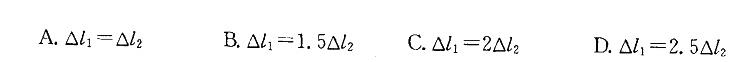
 分别计算杆①和杆②的伸长量,再加以比较,可以得到结论。
分别计算杆①和杆②的伸长量,再加以比较,可以得到结论。