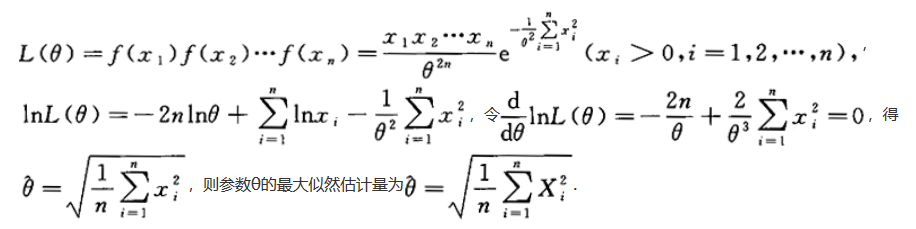第1题:
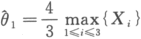 :与
:与 都是参数θ的无偏估计量,试比较其有效性.
都是参数θ的无偏估计量,试比较其有效性.

第2题:
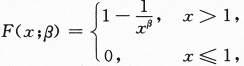

第3题:


第4题:
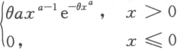 ,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.
,θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.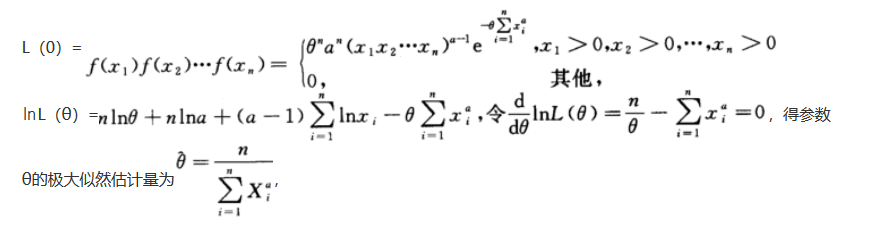
第5题:
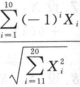 所服从的分布.
所服从的分布.
第6题:
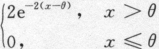 ,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
第7题:

第8题:
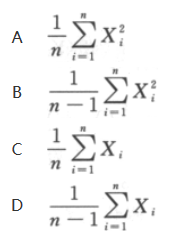
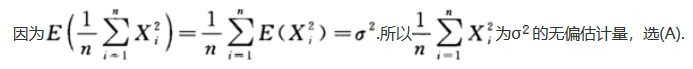
第9题:
 P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.
P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.第10题:
 ,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.