多个结点具有的子树标为该结点的度。

若一颗二叉树中只有叶结点和左右子树皆非空的结点，设叶结点的个数为n，则左右子树皆非空的结点个数为__________。

多个结点具有的子树标为该结点的度。

此题为判断题(对，错)。

在平衡二叉树中，(55)。

A．任意结点的左、右子树结点数目相同

B．任意结点的左、右子树高度相同

C．任意结点的左、右子树高度之差的绝对值不大于1

D．不存在度为1的结点

有一个深度为4的满二叉树，下面关于序号为7的结点的叙述中正确的是（ ）。

A．该结点双亲的序号为4

B．该结点处于二叉树的第4层

C．该结点没有右子树

D．该结点左子树根结点的序号为14

A.左子树的叶子结点

B.左子树的分支结点

C.右子树的叶子结点

D.右子树的分支结点

A、该结点的子树的个数

B、树中结点度的最大值

C、代表树中的一个数据元素

对一棵二叉树的中序遍历序列中，根结点右边的结点属于( )。

A．左子树上的叶子结点

B．右子树上的所有结点

C．左子树上的所有结点

D．右子树上的叶子结点

己知一棵度为3的树(一个结点的度是指其子树的数目，树的度是指该树中所有结点的度的最大值)中有5个度为1的结点，4个度为2的结点，2个度为3的结点，那么，该树中的叶子结点数目为(61)。

A．10

B．9

C．8

D．7

阅读以下说明和C语言函数，将应填入(n)处的字句写在答题纸的对应栏内。

【说明】

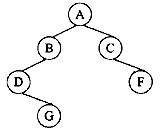
一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左

子树分支向下查找，直到某个结点不存在左子树时为止，该结点即为此二叉树的“最左下”结点。例如，下图所示的以 A为根的二叉树的“最

左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。

二叉树的结点类型定义如下：

typedef stmct BSTNode{

int data；

struct BSTNode*lch,*rch；//结点的左、右子树指针

}*BSTree；

函数BSTree Find Del(BSTree root)的功能是：若root指向一棵二叉树的根结点，则找出该结点的右子树上的“最左下”结点*p，并从

树于删除以*p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

BSTrce Find_Del(BSTreeroot)

{ BSTreep,pre；

if ( !root ) return NULL； /*root指向的二叉树为空树*/

(1)； /*令p指向根结点的右子树*/

if ( !p ) return NULL；

(2)； /*设置pre的初值*/

while(p-＞lch){ /*查找“最左下”结点*/

pre=p；p=(3)；

}

if ((4)==root) /*root的右子树根为“最左下”结点*/

pre-＞rch=NULL；

else

(5)=NULL； /*删除以“最左下”结点为根的子树*/

reurn p；

}

A、(n(k+1)-1)/k

B、(n(k+1)+1)/k

C、(n(k-1)+1)/k

D、(n(k-1)-1)/k