小一同学在做出一道数学题后高兴不已,其动机属于()
第1题:
第2题:
第3题:
王老师让小明、小强和小刚三位同学同时做一道有关百分数的应用题,小明同学几乎立即就解决了问题;小强同学在吃力地尝试做,但没有解决;小刚同学尝试了一下就放弃努力,双臂无力地垂下,眉头紧皱。看到这种情况,王老师让小明同学向小强、小刚同学说出了自己的解题过程后,又出了一道类似的题目,小强同学很快就掌握了,而小刚同学还是一筹莫展。
请结合教育心理学的教学心理中的有关知识对上面的这种问题加以分析并谈谈自己对这个问题的做法。
答案:(1)这个问题可以用维果斯基提出的“最近发展区”的观点加以解释。
( 2 )最近发展区是指儿童能够独立完成的学习任务水平与在有能力的教师或同伴的帮助下方能完成的学习任务水平之间的区域。
( 3 )这三个学生在教学中所表现出的学习能力是不同的。小明的能力在这道数学题的最近发展区之上,他不需要额外的帮助;小刚的能力在最近发展区之下,即使在同学的帮助下,他也没能完成百分数问题的学习;小强的能力恰好处在最近发展区之内,在同学的帮助下,他成功地完成了学习任务。
( 4 )最近发展区代表着一种学习情况,在该情况中,教师与学生共同努力便能促进学生学习的发展。
对于这个问题的做法:因三人的能力差异,需要因材施教。可以让小明做难度较高的百分数引申题,小强仍做这道题,小刚做难度稍低的百分题。
第4题:
体育教育专业王同学因为特别喜欢网球,因此在选择专项时自然选择了网球,它产生这一行为的动机属于()
第5题:
黑猩猩在高兴的时候会做出怎样的表情?()
第6题:
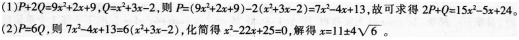
第7题:
关于拉伸时各道次变形程度的分布,下列说法不正确的是()。
第8题:
A、心境
B、激情
C、美感
D、理智感
第9题:
我国的古代数学成就辉煌灿烂,请看一道古代的数学题:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
第10题:
在200米比赛中,甲同学(第二道)的起点在乙同学(第一道)起点的前面这是因为()