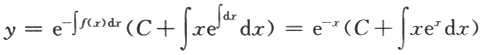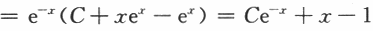若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。
第1题：
，则
第2题：
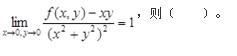
第3题：
A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.
B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.
C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.
D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
第4题：
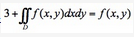，其中D是由x轴、y轴、
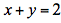所围成的闭区域
第5题：
第6题：
, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是
第7题：
第8题：
第9题：
第10题：
