在训练学生估计平行四边形面积后,要求学生估计长方形和不规则图形面积,对长方形面积的估计成绩显著提高,而对不规则图形面积的估计则没有提高。这一实验结果支持了()。
第1题:
学生学习完平行四边形后再学习长方形,平行四边形的学习对学习长方形的影响是:( )
A顺向正迁移
B顺向负迁移
C逆向正迁移
D逆向负迁移
第2题:
A、能描述出实物或图形的运动和变化
B、使学生获得有关线、角、简单平面图形和立体图形的知觉映象
C、使学生能建立有关长度、面积或体积等的基本概念
D、能够对不太远的物体间的方位、距离和大小有较正确的估计
E、能从较复杂的图形中辨别有各种特征的图形
第3题:
依上述资料该地区对参加高考的学生中买了假冒2B铅笔的学生比例作出点估计和以95%(t=1.96)的可靠程度作区间估计的结果是( )。
A.点估计为4%
B.点估计为6%
C.区间估计为0.86%至7.1%之间
D.区间估计为最多不会超过30%
第4题:
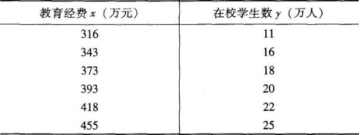
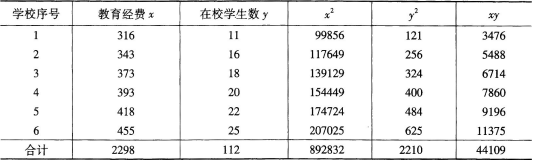
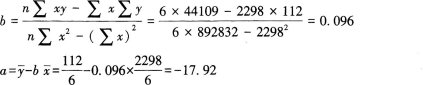
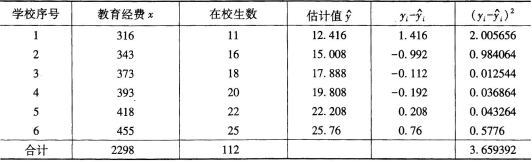
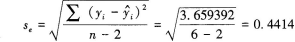
第5题:
第6题:
平行四边形面积公式推导的教学片断:(1)教师布置学生独立思考的内容:我们如何把平行四边形转化为已经知道面积公式的平 面图形来研究它的面积公式呢?(2)学生合作交流不到2分钟,当教师发现有一个小组的同学“过平行四边形的一个顶点 作平行四边形的高,把平行四边形分割成一个直角三角形和一个直角梯形,然后再等量拼成一个长方形.所以平行四边形的面积就是底乘高”的方法后,就立即宣布合作结束。。问题:从与合作学习有关的因素的角度分析本材料。
第7题:
第8题:
教学设计一:在教学求平行四边形面积时,教师讲授如下:连接AC,因为三角形ABC与三角形CDA的三边分别相等,所以,这两个三角形全等,三角形ABC的面积等于1/2底乘高,所以,平行四边形ABCD的面积等于底乘高,命题得到证明。然后,教师列举很多不同大小的平行四边形,要求学生求出它们的面积,结果每个问题都正确解决了。下课前,教师又布置了十几个类似的问题作为家庭作业。
教学设计二:教师引导学生分析问题,即如何把一个平行四边形转变成一个长方形,然后组织学生自主探究,并获得计算平行四边形面积的公式。
问题:两则教学设计中教师的教学方法有何不同?两种教学方法对学生的学习将产生怎样的影响?
第9题:
第10题: