每次把待排序方的区间划分为左、右两个区间，其中左区间中元素的值不大于基准元素的值，右区间中元素的值不小于基准元素的值，此

在快速排序过程中，每次划分，将被划分的表(或子表)分成左、右两个子表，考虑这两个子表，下列结论一定正确的是________。

A．左、右两个子表都已各自排好序

B．左边子表中的元素都不大于右边子表中的元素

C．左边子表的长度小于右边子表的长度

D．左、右两个子表中元素的平均值相等

阅读以下说明和代码，填补代码中的空缺，将解答填入答题纸的对应栏内。 【说明】 下面的程序利用快速排序中划分的思想在整数序列中找出第k小的元素（即将元素从小到大排序后，取第k个元素）。 对一个整数序列进行快速排序的方法是：在待排序的整数序列中取第一个数作为基准值，然后根据基准值进行划分，从而将待排序的序列划分为不大于基准值者（称为左子序列）和大于基准值者（称为右子序列），然后再对左子序列和右子序列分别进行快速排序，最终得到非递减的有序序列。 例如，整数序列“19, 12, 30, 11,7,53, 78, 25"的第3小元素为12。整数序列“19,12,7,30,11,11,7,53,78,25,7"的第3小元素为7。 函数partition（int a[ ], int low,int high）以a[low]的值为基准，对a[low]、a[low+1]、…、 a[high]进行划分，最后将该基准值放入a[i] (low≤i≤high)，并使得a[low]、a[low+1]、，．．、 A[i-1]都小于或等于a[i]，而a[i+1]、a[i+2]、．．、a[high]都大于a[i]。 函教findkthElem(int a[],int startIdx,int endIdx,inr k)在a[startIdx]、a[startIdx+1]、...、a[endIdx]中找出第k小的元素。

【代码】 include <stdio.h> include <stdlib.h> Int partition（int a [ ]，int low, int high） {//对 a[low..high]进行划分，使得a[low..i]中的元素都不大于a[i+1..high]中的元素。 int pivot=a[low]； //pivot表示基准元素 Int i=low,j=high; while(（ 1） ){ While(i<j&&a[j]>pivot)--j; a[i]=a[j] While(i<j&&a[i]<=pivot)++i; a[j]=a[i] } （2） ； //基准元素定位 return i； } Int findkthElem（int a[ ]，int startIdx，int endIdx, int k） {//整数序列存储在a[startldx..endldx]中，查找并返回第k小的元素。 if (startldx<0 ||endIdx<0 || startIdx>endIdx || k<1 ||k-1>endIdx ||k-1<startIdx) Return-1; //参数错误 if(startIdx<endldx){ int loc=partition(a, startIdx, endldx)； ∥进行划分，确定基准元素的位置 if (loc==k-1) ∥找到第k小的元素 return （3） ； if(k-1 <loc) //继续在基准元素之前查找 return findkthElem(a, （4） ,k）； else ／／继续在基准元素之后查找 return findkthElem(a， （5） ，k); } return a[startIdx]； } int main() { int i, k; int n; int a[] = {19, 12, 7, 30, 11, 11, 7, 53, 78, 25, 7}; n= sizeof(a)／sizeof(int) //计算序列中的元素个数 for (k=1;k＜n+1；k++){ for(i=0;i＜n;i++){ printf(“%d/t”,a[i]); } printf(“\n”); printf(“elem %d=%d\n,k,findkthElem(a,0,n-1,k));//输出序列中第k小的元素 } return 0； }

A.分治

B.动态规划

C.贪心

D.回溯

阅读以下说明和 C 代码，填补代码中的空缺，将解答填入答题纸的对应栏内。 【说明】 对一个整数序列进行快速排序的方法是：在待排序的整数序列中取第一个数作为基准值，然后根据基准值进行划分，从而将待排序列划分为不大于基准值者(称为左子序列)和大于基准值者(称为右子序列)，然后再对左子序列和右子序列分别进行快速排序， 最终得到非递减的有序序列。 函数 quicksort(int a[]，int n)实现了快速排序，其中，n 个整数构成的待排序列保存在数组元素 a[0]-a[n-1]中。

【C 代码】 include < stdio.h> void quicksort(int a[] ，int n) { int i ，j; int pivot = a[0]; //设置基准值 i =0; j = n-l; while (i< j) { while (i<j &&（1）) j-- //大于基准值者保持在原位置 if (i<j) { a[i]=a[j]; i++;} while (i,j &&（2）) i++; //不大于基准值者保持在原位置 if (i<j) { a[j]=a[i]; j--;} } a[i] = pivot; //基准元素归位 if ( i>1) （3） ; //递归地对左子序列进行快速排序 if ( n-i-1>1 ) （4） ; //递归地对右子序列进行快速排序 } int main () { int i，arr[ ] = {23，56，9，75，18，42，11，67}; quicksort ( （5） ); //调用 quicksort 对数组 arr[ ]进行排序 for( i=0; i<sizeof(arr) /sizeof(int); i++ ) printf(" %d\t" ，arr[i]) ; return 0; }

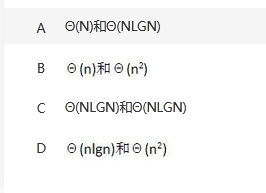
快速排序算法在排序过程中，在待排序数组中确定一个元素为基准元素，根据基准元素把待排序数组划分成两个部分，前面一部分元素值小于等于基准元素，而后面一部分元素值大于基准元素。然后再分别对前后两个部分进一步进行划分。根据上述描述，快速排序算法采用了 (61) 算法设计策略。已知确定基准元素操作的时间复杂度为，则快速排序算法的最好和最坏情况下的时间复杂度为 (62) 。

A.分治

B.动态规划

C.贪心

D.回溯

A、快速排序

B、冒泡排序

C、简单选择排序D、归并排序