Q1=Q2=10
Q1=5
Q1=Q2=15
Q1=Q2
第1题:
设两个寡头构成的总市场需求曲线为P=30-Q式中,Q=Q1+Q2,假设MC1=M当达到均衡状态时,每个厂商的产量为().
A.Q1=Q2=10
B.Q1=5
C.Q1=Q2=15
D.Q1=Q2
第2题:
假设在完全竞争行业中有许多相同的厂商,代表性厂商LAC曲线的最低点的值为6美元,产量为500单位;当工厂产量为550单位的产品时,各厂商的SAC为7美元;还知市场需求函数与供给函数分别是:QD=80000-5000P、QS=35000+2500P(1)求市场均衡价格,并判断该行业是长期还是在短期处于均衡?为什么?(2)在长期均衡时,该行业有多少家厂商?(3)如果市场需求函数发生变动,变为Q′d=95000-5000P,试求行业和厂商的新的短期的均衡价格及产量,厂商在新的均衡点上,盈亏状况如何?
(1)已知市场需求函数与供给函数分别为:QD=80000-5000P和QS=35000-2500P,市场均衡时QD=QS即80000-5000P=35000-2500P,所以市场均衡价格P=6(美元),这与代表性厂商LAC曲线最低点的值(6美元)相等。故该行业处于长期均衡状态。
(2)长期均衡价格P=6美元时,则长期均衡产量QS=QD=80000-5000×6=50000(单位)而长期均衡时每家厂商的产量为500单位,故该行业厂商人数为n=50000/500=100,即该行业有100有厂商。
(3)新的需求函数为Q′d=95000-5000P,但供给函数仍为QS=35000+2500P。新的市场均衡时Q′D=QS,即95000-5000P=35000+2500P,因而新的市场均衡价格P=8美元(也即行业短期均衡价格),行业短期均衡产量为:Q′d=QS=35000+2500×8=55000。在短期,厂商数不会变动,故仍是100家,因此,在新的均衡中,厂商产量Q/N=55000/100=550。从题中假设知道,当产量为550单位时,厂商的SAC为7美元。可见,在短期均衡中价格大于平均成本,厂商有盈利,利润为π=(P-SAC.Q=(8-7)×550=550(美元)
第3题:
计算题:
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:
(1)当市场商品价格为P=100时,厂商实现MR=LMC时的产量,平均成本和利润;
(2)该行业长期均衡时的价格和单个厂商的产量;
(3)当市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
(1)P=MR=LMC=dLTC/dQ=3Q2-24Q+40=100
Q=10
LAC=LTC/Q=Q2-12Q+40
=100-120+40=20
利润=TR-TC=PQ-(Q3-12Q2+40Q)=800
(2)长期均衡的条件为LAC=LMC=P即位于LAC的最低点
LAC=LTC/Q=Q2-12Q+40
最低点时Q=6LAC最小为4
即当价格为4时,行业实现长期均衡,其产量为6
(3)行业的长期供给函数为P=4需求函数为Q=660-15P当供给和需求等时行业实现均衡产量为Q=660-15*4=600每一个厂商的产量为6所以厂商数量为100。
第4题:
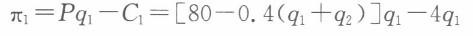
第5题:

第6题:
某成本不变的完全竞争行业的代表性厂商的长期总成本函数为LTC=Q3-60Q2+1500Q,产品价格P=975美元,市场需求函数为P=9600-2Q,
试求:
(1)利润极大时的产量、平均成本和利润。
(2)该行业长期均衡时的价格和厂商的产量。
(3)用图形表示上述(1)和(2)。
(4)若市场需求曲线是P=9600-2Q,试问长期均衡中留存于该行业的厂商人数是多少?
1)LMC=dLTC/dQ=3Q2-120Q+1500
当LMC=P=MR时,利润极大。
故,3Q2-120Q+1500=975,得Q1=5(舍);Q2=35
LAC=LTC/Q=Q2-60Q+1500=352+60×35+1500=625
π=TR-TC=P·Q-AC·Q=975×35-625×35=12250
(2)行业长期均衡时,LAC最小,当LAC′=0,且LAC〞>0时,有最小值。
即,(Q2-60Q+1500)′=2Q-60=0,得,Q=30,LAC〞=2>0
当Q=30时,P=LACmin=302-60×30+1500=600
(3)如图所示:


(4)若市场需求曲线是P=9600-2Q,又知长期均衡价格P=600,
业产量Q=(9600-P)/2=(9600-600)/2=4500
厂商人数N=行业产量/厂商产量=4500/30=150家
第7题:
在伯特兰寡头市场上,有两个厂商,其边际成本均为20,市场需求曲线为P=50-Q,均衡的市场价格为()。
A、10
B、20
C、30
D、40
第8题:
假设双寡头面临如下一条线性需求曲线:P=30-Q,Q表示两厂商的总产量,即Q=Q再假设边际成本为0。企业1是先行的主导企业,企业2是追随企业,达到均衡解时,两个厂商的产量分别为().
A.Q1=Q2=10
B.Q1=5
C.Q1=Q2=15
D.Q1=15,Q2=5
第9题:

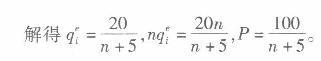
第10题:
