若α1,α2,…,αs线性相关,则Aα1,Aα2,…,Aαs线性相关
若α1,α2,…,αs线性相关,则Aα1,Aα2,…,Aαs线性无关
若α1,α2,…,αs线性无关,则Aα1,Aα2,…,Aαs线性相关
若α1,α2,…,αs线性无关,则Aα1,Aα2,…,Aαs线性无关
第1题:
第2题:

第3题:


第4题:

第5题:

第6题:
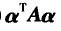


第7题:

第8题:
第9题:
 .其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
.其中A*是矩阵A的伴随矩阵,E是n阶单位矩阵. (1)计算并化简PQ; (2)证明:矩阵Q可逆的充分必要条件是.
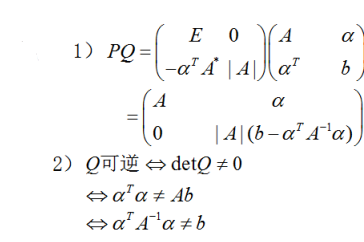
第10题: