违法和不良信息举报 联系客服
免费注册 登录

单选题微分方程y″－2y′＋y＝0的两个线性无关的特解是（　　）。[2016年真题]A y1＝x，y2＝exB y1＝e－x，y2＝exC y1＝e－x，y2＝xe－xD y1＝ex，y2＝xex

题目
单选题
微分方程y″－2y′＋y＝0的两个线性无关的特解是（　　）。[2016年真题]
A

y1＝x，y2＝ex

B

y1＝e－x，y2＝ex

C

y1＝e－x，y2＝xe－x

D

y1＝ex，y2＝xex

如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

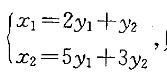如果从变量y1,y2到x1,x2的线性变换是，则变量x1,x2到变量y1,y2的线性变换是：


答案：A
解析：

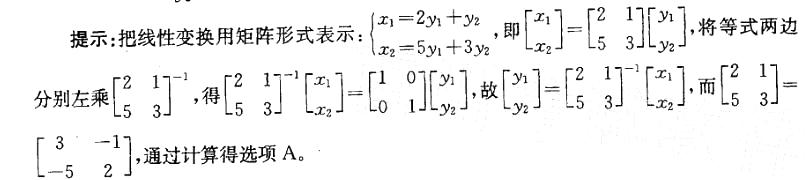
第2题：

如果业务Y1和业务Y2具有替代性，当Y1资费降低而Y2资费不变时，必然导致( )。

A:Y1业务量降低
B:Y2业务量的提高
C:Y1收入的降低
D:Y2业务量的降低

答案：D
解析：
本题考查对线性从量资费特点的理解。线性从量资费当一方资费下降，另一方不变时，必然导致下降方业务量增长，不变方业务量下降。

第3题：

已知“a=dict(x=1,y=dict(y1=2,y2=3))”且“b=a.copy()”,则执行“a['y']['y1']=10”后,则print(b)的输出结果为()。

A、{x=1,y={y1=10,y2=3}}

B、{x=1,y={y1=2,y2=3}}

C、{'x':1,'y':{'y1':10,'y2':3}}

D、{'x':1,'y':{'y1':2,'y2':3}}


参考答案：C

第4题：

若y1（x）是线性非齐次方程y '+ p（x）= Q（x）的解，y1（x）是对应的齐次方程y'+p（x）y=0的解，则下列函数中哪一个是y '+ p（x）y= Q（x）的解？

A. y=cy1（x）+y2（x）
B. y=y1（x）+c2y2（x）
C. y=c[y1 （x）+y2（x）]
D.y=c1y（x）-y2（x）

答案：A
解析：
提示：由一阶线性非齐次方程通解的结构确定，即由对应齐次方程的通解加上非齐次的一特解组成。

第5题：

以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是:

A. y''-2y'-3y=0
B. y''+2y'-3y=0
C. y''-3y'+2y=0
D. y''+2y'+y=0

答案：B
解析：
提示 y''-3y'+2y=0→r2+2r-3 = 0→r1=-3，r2=1，所以y1=ex，y2=e-3x，选项B的特解满足条件。

第6题：

设非齐次线性微分方程y´+P(x)y=Q(x)有两个不同的解析：y1(x)与y2(x)，C为任意常数，则该方程的通解是( ).

A.C[(y1(x)-y2(x)]
B.y1(x)+C[(y1(x)-y2(x)]
C.C[(y1(x)+y2(x)]
D.y1(x)+C[(y1(x)+y2(x)]

答案：B
解析：
y1(x)-y2(x)是对应的齐次方程y

第7题：


A、 y1=x，y2=ex
B、 y1=e-x，y2=ex
C、 y1=e-x，y2=xe-x
D、 y1=ex，y2=xex

答案：D
解析：

第8题：

●分别运行下列两段程序后，y1和y2的值是(39)。

程序段1：

#define f(x) x*x

floatX，y1；

X=2.0；

Y1=x/f(x);

程序段2：

#define f(x) (x*x)

floatx，y2;

X=2.0；

y2=x/f(x);，

( 39)A.y1=2.0,y2=0.5

B.y1=0.5,y2=2.0

C. y1=2.0,y2=1.0

D. y1=1.0,y2=2.0


正确答案：A

第9题：

设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x)，y2(x)，C为任意常数，则该方程通解是( )。

A.C[y1(x)-y2(x)]
B.y1(x)+C[y1(x)-y2(x)]
C.C[y1(x)+y2(x)]
D.y1(x)+C[y1(x)+y2(x)]

答案：B
解析：
因为y1(x)，y2(x)是y′+P(x)y=Q(x)的两个不同的解，所以C(y1(x)-y2(x))是齐次方程y′+P(x)y=0的通解，进而y1(x)+C[y1(x)-y2(x)]是题中非齐次方程的通解。

第10题：

若y2(x)是线性非齐次方程y'+p(x)y=q(x)的解，y1(x)是对应的齐次方程y'+p(x)y=0的解，则下列函数也是y'+p(x)y=q(x) 的解的是（ ）。
A.y=Cy1(x)+y2(x) B. y=y1(x)+Cy2(x)
C.y=C[y1(x)+y2(x)] D.y=Cy1(x)-y2(x)


答案：A
解析：
提示：齐次方程的通解加上非齐次的特解仍是非齐次的解。

更多相关问题
相关内容