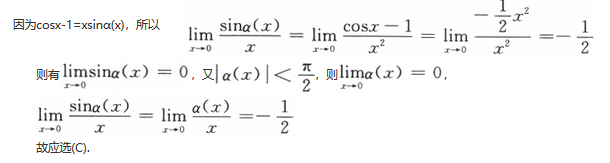f（x）与x是等价无穷小量
f（x）与x是同阶但非等价无穷小量
f（x）是比x较高阶的无穷小量
f（x）是比x较低阶的无穷小量
第1题：
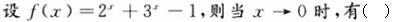
第2题：
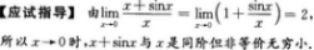
第3题：
A、高阶无穷小
B、低阶无穷小
C、等价无穷小
D、同阶但不等价无穷
第4题：
第5题：
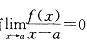，则当x→a 时，f(x)是：
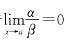，称在x→a时，a是β的高阶无穷小，所以答案D成立。f(x)是比(x-a)高阶的无穷小。第6题：
则当x→0时，f(x)是：
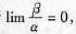就称β是比α高阶的无穷小，记作β=σ（α），并称α是比β低阶的无穷小
就称β是与α高阶的无穷小
就称β是与α等价的无穷小，记作α~β，关于等价无穷小，有以下性质：
且
存在，则
第7题：
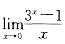的极限判断。第8题：
A、φ与ψ为等价无穷小
B、φ是比ψ为较高阶的无穷小
C、φ是比ψ为较低阶的无穷小
D、φ与ψ是同价无穷小
第9题：
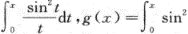(x－t)dt,则当x→0时,g(x)是f(x)的().
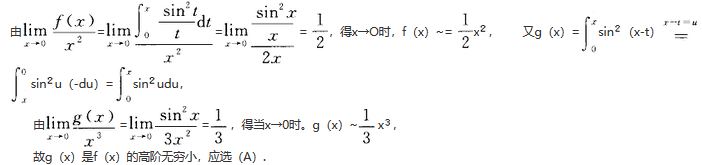
第10题：
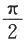，则当x→0时，α(x)是
