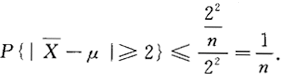违法和不良信息举报 联系客服
免费注册 登录

问答题设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。

题目
问答题
设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。
如果没有搜索结果或未解决您的问题，请直接 联系老师 获取答案。
相似问题和答案

第1题：

设X1，X2，…，Xn是简单随机样本，则有( )。

A．X1，X2，…，Xn相互独立

B．X1，X2，…，Xn有相同分布

C．X1，X2，…，Xn彼此相等

D．X1与(X1+X2)/2同分布

E．X1与Xn的均值相等


正确答案：ABE
解析：简单随机样本满足随机性和独立性，且每一个样本都与总体同分布，样本均值相等。

第2题：

设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.


答案：
解析：

第3题：

设X1，X2，…，Xn是简单随机样本，则有( )。

A．X1，X2，…，Xn相互独立

B．X1，X2，…，Xn有相同分布

C．X1，X2，…，Xn彼此相等

D．X1与(X1+X2)/2同分布

E．X1与X2的均值相等


正确答案：ABE
解析：满足随机性和独立性的样本称为简单随机样本，简称随机样本。随机样本X1，X2，…，Xn可以看做n个相互独立的、同分布的随机变量，每一个的分布与总体分布相同。

第4题：

设X1,X2,…,Xn是来自总体X的简单随机样本,已知E(X^k)=ak(k=1,2,3,4).
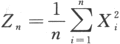　　证明：当n充分大时,随机变量近似服从正态分布,并指出其分布参数.


答案：
解析：

第5题：

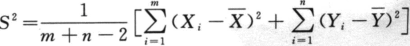设总体X,Y相互独立且都服从N（μ,σ^2）分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明：为参数σ^2的无偏估计量,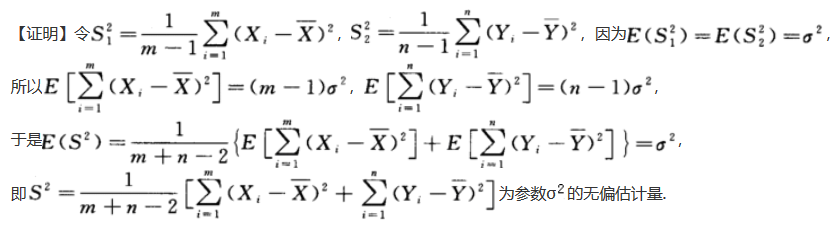


答案：
解析：

第6题：

设X1,X2,…Xn是简单随机样本，则有（ ）。
A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
E.X1与Xn的均值相等


答案：A,B,E
解析：
简单随机样本满足随机性和独立性，且每一个样本都与总体同分布，样本均值相等。

第7题：

设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时，依概率收敛于_______.


答案：
解析：
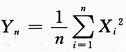本题是数三的考题，根据切比雪夫大数定律或者辛钦大数定律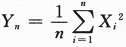，依概率收敛于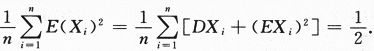答案应填

第8题：

设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。

A．有相同的数学期望

B．有相同的方差

C．服从同一指数分布

D．服从同一离散型分布


正确答案：C

第9题：

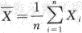设x为一个总体且E(x)=k,D(x)=1,X1,X2,…,xn为来自总体的简单随机样本,令,问n多大时才能使P?


答案：
解析：
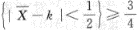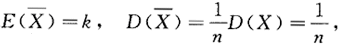由切比雪夫不等式得

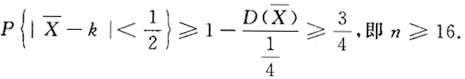
第10题：

若随机变量x1,x2,…,xn相互独立同分布于N{μ,2^2},则根据切比雪夫不等式得P{｜x－μ｜≥2）≤_______.


答案：
解析：
因为X1，X2…，Xn相互独立同分布于N（μ，2^2），所以，从而

更多相关问题
相关内容